Wichita State University Logo

Math 344: Calculus III

13.1 Vector Functions and Space Curves

13.1.1 Vector-Valued Functions ¶

As mentioned in a previous section , a mathematical function is defined by a its domain , codomain , and the assignment relation . We a call a function a vector function or vector-valued function if its codomain is a vector. In this section, we will focus on vector functions whose codomains are three-dimensional. For instance, let $\mathbf{r}$ be a vector function mapping $\mathbb{R}$ onto $\mathbb{R}^3$

$$ \mathbf{r}(t) : \mathbb{R}\rightarrow\mathbb{R}^3 $$
given by

$$ \def\ihat{\mathbf{\hat{\mmlToken{mi}[mathvariant="bold"]{ı}}}} \def\jhat{\mathbf{\hat{\mmlToken{mi}[mathvariant="bold"]{ȷ}}}} \def\khat{\mathbf{\hat{k}}} \mathbf{r}(t) = \left\langle\, f(t),g(t),h(t)\,\right\rangle = f(t)\ihat + g(t)\jhat + h(t)\khat $$
Here $f$, $g$, and $h$ are all real-valued functions of one variable (the kind you are used to thinking about). In this usage, we call them component functions of $\mathbf{r}$. It is common to use the independent variable $t$ since most application problems depend upon time.

Example 13.1.1 ¶

Let

$$ \mathbf{r}(t) = \left\langle\, \sin t,\sqrt{2-t},\ln t\,\right\rangle $$
whose component functions are

$$ f(t) = \sin t\qquad\qquad g(t) = \sqrt{2-t} \qquad\qquad h(t) = \ln t $$
The domain is not explicitly given for this function but, as is typical, we assume that the domain is as large as possible by examining the component functions. The component function $f$ is defined for all $t$, $g$ is defined for all $t\leq 2$, and $h$ is defined for all $t\gt 0$. By taking the intersection of all three of these component function domains, the domain of $\mathbf{r}$ is $(0,2]$.

13.1.2 Limits and Continuity ¶

Any discussion of calculus requires the notion of a limit, and since our goal is to discuss vector calculus we have to understand limits in the context of vector functions. We can understand them in two ways. First, the $\epsilon$-$\delta$ definition of a limit

Definition of a Limit ¶

We say that

$$ \lim_{t\rightarrow t_0} \mathbf{r}(t) = \mathbf{L} $$
if and only if for each $\epsilon\gt 0$ there is a $\delta\gt 0$ such that $0\lt |t - t_0|\lt \delta$ implies that $|\mathbf{r}(t) - \mathbf{L}| \lt\epsilon$.

This definition is just a vector function extension of the familiar version for one-dimensional functions. The only difference is that instead of $\epsilon$ giving an interval for the outputs, it defines an "$\epsilon$ ball" that the limit must end up in to exist.

More practically, we can also use a component-wise limit for vector functions of a single input variable.

Definition of a Limit (Alternative) ¶

Let $\mathbf{r}(t) = \left\langle\, f(t),g(t),h(t)\,\right\rangle$, then
$$ \lim_{t\rightarrow t_0} \mathbf{r}(t) = \left\langle\, \lim_{t\rightarrow t_0} f(t),\, \lim_{t\rightarrow t_0} g(t)\,, \lim_{t\rightarrow t_0} h(t)\,\right\rangle $$
if the limits of each component $f$, $g$, and $h$ all exist.

Exercise 13.1.1 ¶

Determine $\displaystyle\lim_{t\rightarrow 0} \mathbf{r}(t)$ if

$$ \mathbf{r}(t) = \left\langle\, e^{-3t},\frac{t^2}{\sin^2 t},\cos 2t\,\right\rangle = e^{-3t}\,\ihat + \frac{t^2}{\sin^2 t}\,\jhat + \cos 2t\, \khat $$

Check Your Work

Determine the limit component-wise, noting that two of the three component functions are continuous at zero. Only $\dfrac{t^2}{\sin^2 t}$ is not. To find its limit, we employ the limit properties for exponents and then l'Hospital's rule .

$$ \begin{align*} \lim_{t\rightarrow 0} \dfrac{t^2}{\sin^2 t} &= \lim_{t\rightarrow 0} \left(\dfrac{t}{\sin t}\right)^2 \\ \\ &= \left(\lim_{t\rightarrow 0} \dfrac{t}{\sin t}\right)^2 \quad\color{#0066CC}{\sim\dfrac{0}{0}} \\ \\ &= \left(\lim_{t\rightarrow 0} \dfrac{1}{\cos t}\right)^2 \quad\color{#0066CC}{\text{l'Hospital's Rule}} \\ \\ &= 1 \end{align*} $$
By continuity, $e^{-3(0)} = 1$ and $\cos 2(0) = 1$, so

$$ \lim_{t\rightarrow 0} \mathbf{r}(t) = \langle\,1,1,1\,\rangle = \ihat + \jhat + \khat $$

13.1.3 Parametric Functions ¶

If a vector function of one variable in continuous for all $t$ in an interval $I$, it defines a space curve $C$. $C$ is the set of all points $(x,y,z)\in\mathbb{R}^3$ where

$$ x = f(t)\qquad\qquad y = g(t) \qquad\qquad z = h(t) $$
The equations above are the parametric equations of $C$ where $t$ is the parameter . This curve is associated with a vector function $\mathbf{r}(t) = f(t)\ihat + g(t)\jhat + h(t)\khat$. Most commonly, we think of $(f(t),g(t),h(t))$ as the point in space where a particle is located at time $t$. $\mathbf{r}(t)$ gives us the coordinate vector from the origin to that point. This means that on an interval $I$, the function $\mathbf{r}(t)$ is an arrow whose tip traces out the path of a particle traveling as $t$ varies.

Example 13.1.2 ¶

Let $\mathbf{r}(t) = \sin \pi t\,\ihat - \cos\pi t\,\jhat + \cos\pi t\,\khat$. Using the vector function $\mathbf{r}$, we plot the space curve by drawing $\mathbf{r}(t)$ for many values of $t$ and tracing out the path made by the tip of the arrow, which marks a point $P$ that lies on the curve. In the image below, note that the curve (in blue) has an orientation to it. The arrows on the plotted curve correspond to the direction of increasing $t$. A vector function r(t) and the space curve it traces out. The shape of the traced curve is a tilted ellipse.

Example 13.1.3 ¶

Describe the curve defined by the vector function

$$ \mathbf{r}(t) = \left\langle\, 1-t,3-2t,4+3t\,\right\rangle $$

Solution ¶

From Section 12.5 , we recognize this as a vector equation for a line. We can see that this is equivalent to

$$ \mathbf{r}(t) = \langle\,1,3,4\,\rangle + t\langle\,-1,-2,3\rangle $$

13.1.4 Plane Curves ¶

We may use vector notation to describe plane curves , in particular plane curves that lie on the $xy$-, $xz$-, or $yz$-plane. If curve lies in the $xy$-plane, we just use a vector with two components like

$$ \mathbf{r}(t) = \left\langle\, t^2-1,e^t\,\right\rangle $$
with $\ihat = \langle\,1,0\,\rangle$ and $\jhat = \langle\,0,1\,\rangle$.

We can also think about the projection of a space curve onto the $xy$-, $xz$-, or $yz$-plane. In this case, we have a full 3D vector function and set the unused component to zero (e.g. $z=0$ for the $xy$-plane). In cases where we do not have a computer at our fingertips to determine the behavior of a space curve, we can use the projections of the graphs onto these planes to help us figure out how to draw the space curve.

Exercise 13.1.2 ¶

Let

$$ \mathbf{r}(t) = \left\langle\,t,t,t^2\,\right\rangle $$
Sketch the projections of $\mathbf{r}(t)$ onto each of the $xy$-, $xz$-, or $yz$-planes, then make a sketch of the space curve in 3D.

Plane Projections

A plot of the function < t,t,t^2 > projected onto the xy-, xz-, and yz-planes. These are a line, a parabola, and a parabola respectively.

Space Curve

Three plots of the function < t,t,t^2 > with its projections onto the xy-, xz-, and yz-planes shown.

The perspective is not quite as obvious since the angle used here is oblique, but the shape of the curve as a parabola that lies above the line $y=x$ in the $xy$-plane should be easy to see from the leftmost plot. Note that curve starts far away, then gets nearer to the observer. That will make the projections easier to make sense of.

13.1.5 Intersecting Surfaces ¶

Another way to define a space curve is as the set of points where two surfaces intersect. Given the equations for two surfaces, we determine a parametrization of the curve by generating a vector function from the equations of these surfaces.

Example 13.1.4 ¶

Sketch the curve given by the intersection of the circular cylinder $x^2 + y^2 = 4$ and the parabolic cylinder $z = x^2$. Start by finding the parametric equations, then using a computer to graph the curve.

Solution ¶

We start with the equation of the circular cylinder $x^2 + y^2 = 4$. Since this does not depend on $z$, we can parametrize this equation by letting $z=0$ and using the parametrization of the projection onto the $xy$-plane: $x = 2\cos t$ and $y = 2\sin t$ for a circle of radius $2$. Finding the parametric equation for $z$ is easy, since it only depends on $x$: $z = 4\cos^2 t$. Hence,

$$ x = 2\cos t \qquad\qquad y = 2\sin t \qquad\qquad z = 4\cos^2 t $$
is the set of parametric equations. With these equations, we plot the curve using a computer utility such as Geogebra . 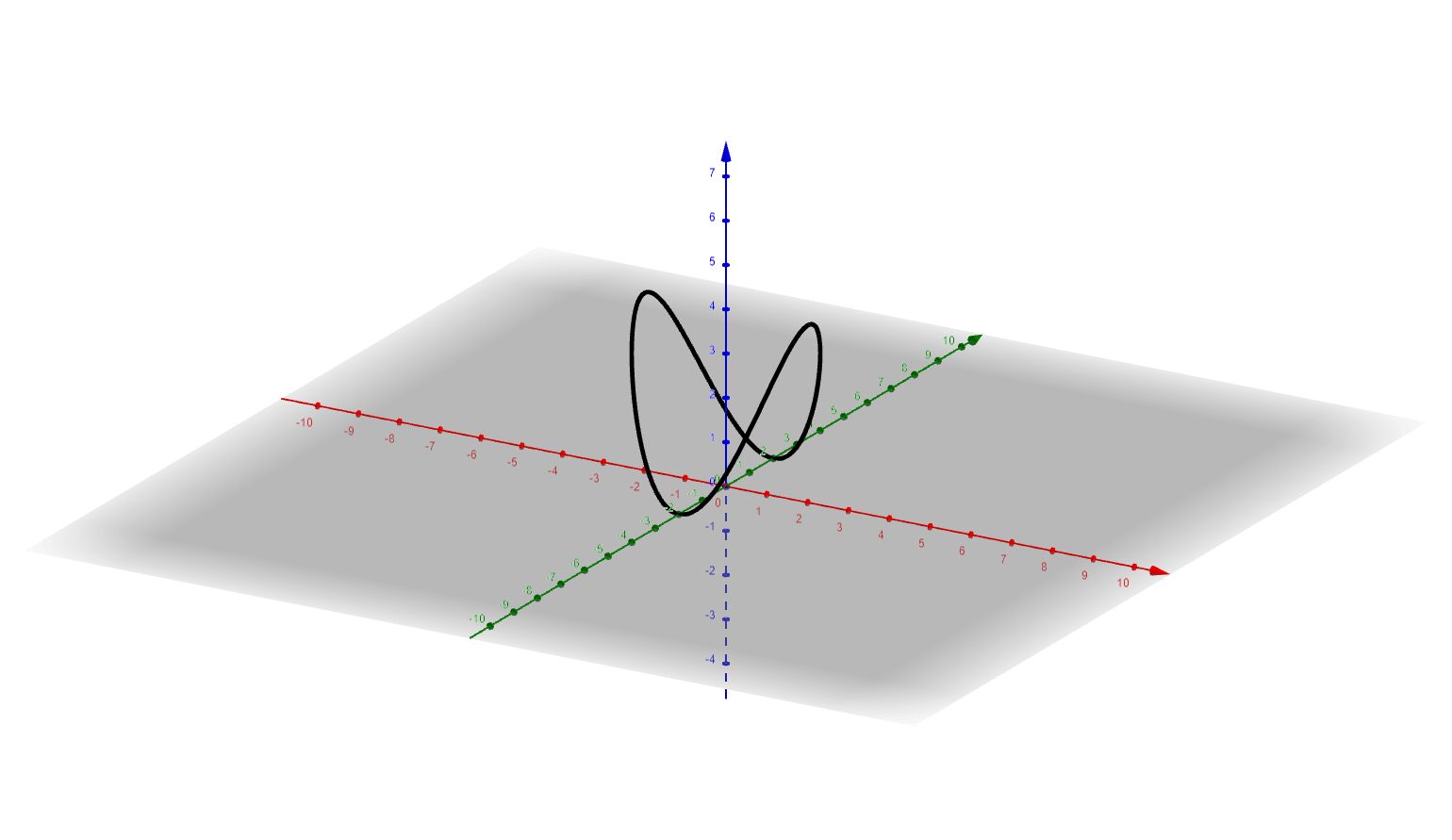A twisted loop in 3D space. Here is a alternative set of plots with the intersecting surfaces shown. A circular cylinder on the left, parabolic cylinder in the middle, and the twisted loop created by the intersection of these two surfaces on the right.

Your use of this self-initiated mediated course material is subject to our Creative Commons License .

Creative Commons Attribution-NonCommercial-ShareAlike 4.0

Creative Commons Logo - Black
Attribution
You must give appropriate credit, provide a link to the license, and indicate if changes were made. You may do so in any reasonable manner, but not in any way that suggests the licensor endorses you or your use.

Creative Commons Logo - Black
Noncommercial
You may not use the material for commercial purposes.

Share Alike
You are free to share, copy and redistribute the material in any medium or format. If you adapt, remix, transform, or build upon the material, you must distribute your contributions under the same license as the original.