Math 344: Calculus III

14.5 The Chain Rule

---

14.5.1 Differentiability of Functions of One Real Variable

In the previous section we discussed linearization of a function, and recalled the linearization of a differentiable function of one real variable using the derivative of such a function at a point $x=a$.

$$ \require{color} \definecolor{brightblue}{rgb}{.267, .298, .812} \definecolor{darkblue}{rgb}{.08, .18, .28} \definecolor{palepink}{rgb}{1, .73, .8} \definecolor{softmagenta}{rgb}{.99,.34,.86} \def\ihat{\mathbf{\hat{\mmlToken{mi}[mathvariant="bold"]{ı}}}} \def\jhat{\mathbf{\hat{\mmlToken{mi}[mathvariant="bold"]{ȷ}}}} \def\khat{\mathbf{\hat{k}}} \newcommand{\pypx}[2][x]{\dfrac{\partial #2}{\partial #1}} \newcommand{\dydx}[2][x]{\dfrac{d #2}{d #1}} \newcommand{\deltax}[2][x]{\frac{\Delta #2}{\Delta #1}} \Delta y = f'(a)(x - a) = f'(a)\Delta x $$
Dividing both sides by $\Delta x$ gives us

$$ f'(a) \approx \deltax{y} = \dfrac{y - f(a)}{x - a} $$
In fact the definition of the derivative of function $f$ and $x=a$ is often given by

$$ f'(a) = L = \displaystyle\lim_{x\rightarrow a} \dfrac{y - f(a)}{x-a} $$
Using the formal definition of limit we have that for every $\varepsilon \gt 0$, there is a $\delta \gt 0$ so that $|x-a|<\delta$ implies

$$ \left|\,\dfrac{y - f(a)}{x-a} - L\,\right| < \varepsilon $$
We can rewrite this equation

$$ \begin{align*} \left| y - f(a) \right| - L|x-a| &\le \left| y - f(a) - L|x-a| \right| \lt \varepsilon|x-a| \\ \\ \left| y - f(a) \right| &\lt \varepsilon|x-a| + L|x-a| \\ \\ \Delta z &= L\Delta x + \varepsilon\Delta x \end{align*} $$
This means that function $f$ is differentiable at $x=a$ if and only if there exists a limit value $L$ such that

$$ \Delta z = L\Delta x + \varepsilon\Delta x, $$
where $\varepsilon(x)\rightarrow 0$ as $\Delta x\rightarrow 0$. Notice that $\varepsilon$ is a function of $x$ and the value of $\varepsilon(x)\rightarrow 0$ as $x\rightarrow a$. However the function $\varepsilon(x)$ does not need to have a value at the point $x=a$. If not, then this is a removable discontinuity and we may define $\varepsilon(a)=0$. This means that we may take the function $\varepsilon(x)$ to be continuous at $x=a$, and $\varepsilon(a)=0$.

If such a limit $L$ exists, then we define $L$ to be $f'(a)$, the derivative of function $f$ at $a$.

14.5.2 The Chain Rule for a Function of One Variable

Let us review the Chain Rule for a function of one real variable. The chain rule governs computing derivatives of the composition of functions. If $y = f(x)$ and $x = g(t)$, then the composition of $f$ and $g$ yields $y = f\left(g(t)\right) = (f\circ g)(t)$. This new function $f\circ g$ is the composition function. If functions $f$ and $g$ are differentiable one may compute the derivative $\frac{dy}{dt} = \frac{d}{dt}(f\circ g)(t)$ using the chain rule

$$ \dydx[t]{y} = \dydx[x]{f}\dydx[t]{x} $$

Example 14.5.1

Suppose $y = \sqrt{x}$ and $x = t^2 + 1$. Then $y = \sqrt{t^2 + 1}$ and

$$ \dydx[t]{y} = \dydx{y}\dydx[t]{x} = \left(\dfrac{1}{2}x^{-1/2}\right)\left(2t\right) = \left(\dfrac{1}{2\sqrt{x}}\right)\left(2t\right) = \dfrac{t}{\sqrt{t^2+1}} $$
Different versions of the chain rule are used to differentiate functions of more than one variable. Each version gives a rule for differentiating a composition of functions.

14.5.3 Differentiability of Functions of Two Variables

Definition

Differentiability for a Function of Two Variables
A function $z = f(x,y)$ is differentiable at $(a,b)$ if $\Delta z$ can be expressed in the form

$$ \begin{align*} \Delta z &= f_x(a,b)\Delta x + f_y(a,b)\Delta y + \varepsilon_1\Delta x + \varepsilon_2\Delta y \\ \\ &= \left(f_x(a,b) + \varepsilon_1\right)\Delta x + \left(f_y(a,b) + \varepsilon_2\Delta y\right) \end{align*} $$
where $\varepsilon_1$ and $\varepsilon_2\ \rightarrow 0$ as $(\Delta x, \Delta y)\rightarrow(0,0)$.

Notice the similarity of this definition of differentiability and the definition used above for a function of one variable. The continuity of the partial derivatives is also important. Furthermore the derivative must converge from all possible directions and along all possible paths on the plane to the point $(a,b)$. Finally the two limits $f_x(a,b)\Delta x + \varepsilon_1\Delta x$ and $f_y(a,b)\Delta y + \varepsilon_2\Delta y$ may not converge at the same rate. Thus we need two different limit functions $\varepsilon_1$ and $\varepsilon_2$.

As in the one dimensional case we may take $\varepsilon_1(x,y)$ and $\varepsilon_2(x,y)$ to both be continuous on a disc containing the point $(a,b)$, and $\varepsilon_1(a,b) = \varepsilon_2(a,b) = 0$.

This definition and the continuity of the partial derivatives ensures differentiability.

Theorem 14.5.1

If the partial derivatives $f_x$ and $f_y$ exist on a disc containing point $(a,b)$ and both partial derivatives are continuous at $(a,b)$, then the function $f$ is differentiable at $(a,b)$.

14.5.4 The Chain Rule for Functions of Two Variables

Theorem 14.5.2

The Chain Rule for a Function of Two Variables (Case 1)
Suppose that $z = f(x,y)$ is a differentiable function of $x$ and $y$, where $x=g(t)$ and $y=h(t)$ are both differentiable functions of $t$. Then $z$ is a differentiable function of $t$ and

$$ \dydx[t]{z} = \pypx{f}\dydx[t]{x} + \pypx[y]{f}\dydx[t]{y} $$

Proof

A change $\Delta t$ in $t$ produces a change in both $\Delta x$ in $x$ and $\Delta y$ in $y$. This in turn produces a change $\Delta z$ in $z$. Since $f$ is differentiable at $(a,b)$ we have

$$ \Delta z = \pypx{f}\Delta x + \pypx[y]{f}\Delta y + \varepsilon_1\Delta x + \varepsilon_2\Delta y $$
where functions $\varepsilon_1$ and $\varepsilon_2$ are continuous on a disc containing the point $(a,b)$, $\varepsilon_1(a,b) = \varepsilon_2(a,b) = 0$, and the two dimensional limit

$$ \displaystyle\lim_{(x,y)\rightarrow(a,b)} \varepsilon_1(x,y) = \displaystyle\lim_{(x,y)\rightarrow(a,b)} \varepsilon_2(x,y) = 0 $$
Dividing both sides of our definition of differentiability by $\Delta t$ yields

$$ \deltax[t]{z} = \pypx{f}\deltax[t]{x} + \pypx[y]{f}\deltax[t]{y} + \varepsilon_1\deltax[t]{x} + \varepsilon_2\deltax[t]{y} $$
Remember that differentiable functions are also continuous. Thus $x = f(t)$ and $y = g(t)$ differentiable implies that they are also continuous. Since

$$ \begin{align*} \Delta x &= g(t + \Delta t) - g(t) \\ \Delta y &= h(t + \Delta t) - h(t) \end{align*} $$
we have that

$$ \begin{align*} \displaystyle\lim_{\Delta t\rightarrow 0}\Delta x &= \displaystyle\lim_{\Delta t\rightarrow 0} g(t + \Delta t) - g(t) = 0 \\ \\ \displaystyle\lim_{\Delta t\rightarrow 0}\Delta y &= \displaystyle\lim_{\Delta t\rightarrow 0} h(t + \Delta t) - h(t) = 0 \\ \end{align*} $$
because $f$ and $g$ are continuous at $t$. Thus $\varepsilon_1$ and $\varepsilon_2\rightarrow 0$ as $\Delta t\rightarrow 0$ because $\Delta x$ and $\Delta y\rightarrow 0$. Also

$$ \begin{align*} \displaystyle\lim_{\Delta t\rightarrow 0}\deltax[t]{x} &= \displaystyle\lim_{\Delta t\rightarrow 0}\dfrac{g(t + \Delta t) - g(t)}{\Delta t} = \dydx[t]{x} = f'(t) \\ \\ \displaystyle\lim_{\Delta t\rightarrow 0}\deltax[t]{y} &= \displaystyle\lim_{\Delta t\rightarrow 0}\dfrac{h(t + \Delta t) - h(t)}{\Delta t} = \dydx[t]{y} = g'(t) \\ \end{align*} $$
because $g$ and $h$ are differentiable at $t$. Hence

$$ \begin{align*} \dydx[t]{z} &= \displaystyle\lim_{\Delta t\rightarrow 0}\ \pypx{f}\deltax[t]{x} + \pypx[y]{f} \deltax[t]{y} + \varepsilon_1\deltax[t]{x} + \varepsilon_2\deltax[t]{y} \\ \\ &= \pypx{f}\dydx[t]{x} + \pypx[y]{f}\dydx[t]{y} + 0\dydx[t]{x} + 0\dydx[t]{y} \\ \\ &= \pypx{f}\dydx[t]{x} + \pypx[y]{f}\dydx[t]{y} \end{align*} $$

Example 14.5.2

Suppose that $z = f(x,y)$ is the surface defined by $z = xy^3 + 2x^3y$, where $x(t) = \cos(t)$ and $y(t) = \sin(t)$. The curve on the surface defined by $z = f\left(\cos(t),\sin(t)\right)$ is differentiable on the interval $[0,2\pi]$ because the two partial derivatives are continuous and the coordinate functions are continuous. Furthermore

$$ \begin{align*} \dfrac{\partial}{\partial t}\,f\left(x(t),y(t)\right) &= \dfrac{dz}{dt} = \left(y^3 + 6x^2y\right)\left(-\sin(t)\right) + \left(3xy^2 + 2x^3\right)\left(\cos(t)\right) \\ \\ &= -\left(\sin^3(t) + 6\cos^2(t)\sin(t)\right)\sin(t) + \left(3\cos(t)\sin^2(t) + 2\cos^3(t)\right)\cos(t) \\ \\ &= -\sin^4(t) - 6\cos^2(t)\sin^2(t) + 3\cos^2(t)\sin^2(t) + 2\cos^4(t) \\ \\ &= 2\cos^4(t) - 3\cos^2(t)\sin^2(t) - \sin^4(t) \\ \\ f'(x(0),y(0)) &= \left.\dfrac{dz}{dt}\right|_{t=0} = 2\cos^4(0) - 3\cos^2(0)\sin^2(0) - \sin^4(0) = 2 \end{align*} $$
This derivative can be interpreted as the instantaneous rate of change of $z$ with respect to $t$ as the point $(x,y)=\left(\cos(t),\sin(t)\right)$ moves along the curve $C$ on the surface $z = xy^3 + 2x^3y$. This curve has the parametric equations

$$ \begin{align*} x &= \cos(t) \\ y &= \sin(t) \\ z &= \cos(t)\sin^3(t) + 2\cos^3(t)\sin(t) \end{align*} $$

The graph of $z = xy^3 + 2x^3y$
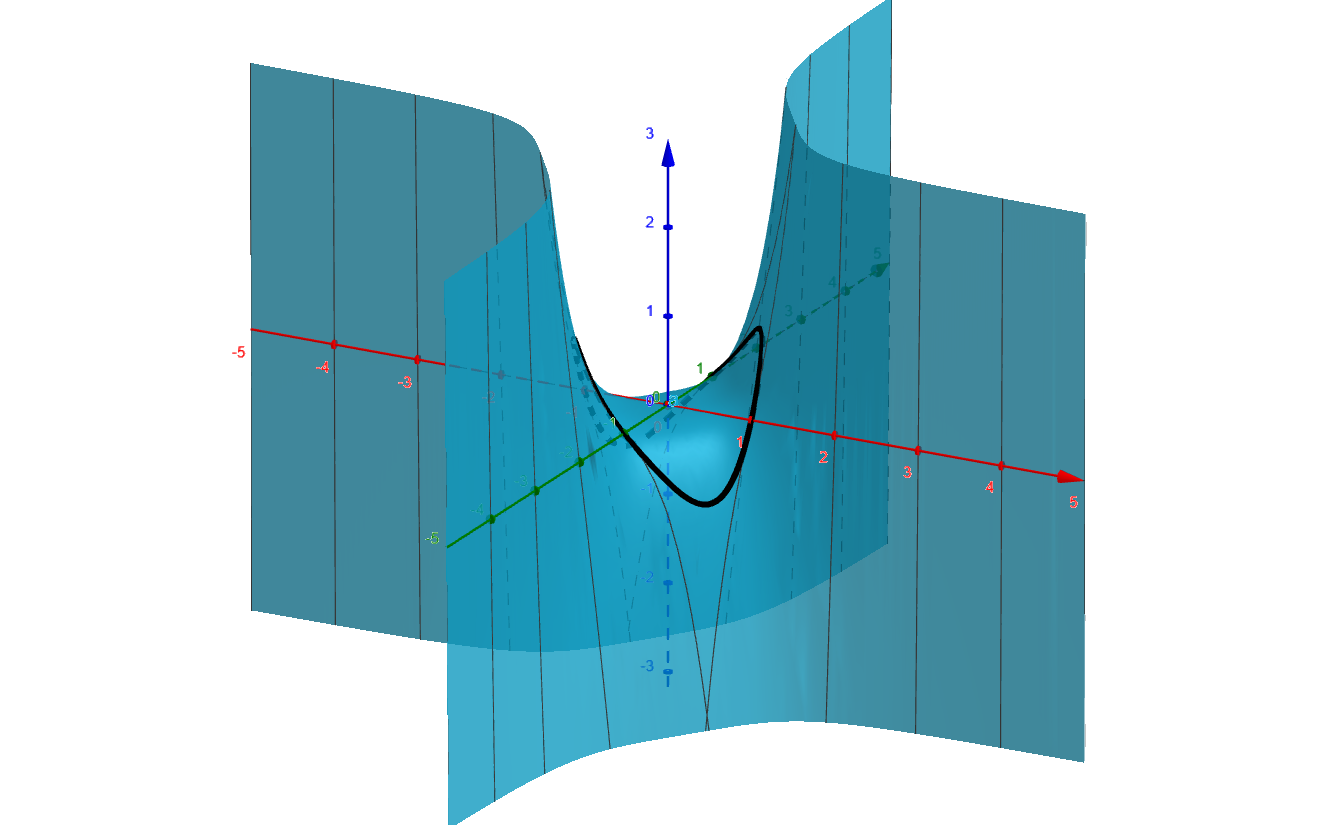
Figure 1

Exercise 14.5.1

Consider the function $z = \sec(x + 2y)$, where $x(t) = t^2$ and $y(t) = \frac{1}{t}$. Compute $\dfrac{dz}{dt}$.

Check your work

$$ \begin{align*} \dfrac{dz}{dt} &= \dfrac{\partial z}{\partial x}\dfrac{dx}{dt} + \dfrac{\partial z}{\partial y}\dfrac{dy}{dt} \\ \\ &= \left(\sec(x+2y)\tan(x+2y)(1)\right)\left(2t\right) + \left(\sec(x+2y)\tan(x+2y)(2)\right)\left(-t^{-2}\right) \\ \\ &= 2\sec(x+2y)\tan(x+2y)\left(t - \dfrac{1}{t^2}\right) \\ \\ &= 2\sec\left(t^2+\frac{2}{t}\right)\tan\left(t^2+\frac{2}{t}\right)\left(t - \dfrac{1}{t^2}\right) \\ \end{align*} $$

14.5.5 A Second Chain Rule for Functions of Two Variables

Theorem 14.5.3

The Chain Rule for a Function of Two Variables (Case 2)
Suppose that $z = f(x,y)$ is a differentiable function of $x$ and $y$, $x = g(s,t)$, and $y = h(s,t)$ are differentiable functions of $s$ and $t$. Consider such a change of variables

$$ z = f(x,y) = f(x(s,t), y(s,t)) = \tilde{f}(s,t) $$
The two first order partial derivatives are given by

$$ \pypx[s]{z} = \pypx{z}\pypx[s]{x}{s} + \pypx[y]{z}\pypx[s]{y},\qquad\qquad \pypx[t]{z} = \pypx{z}\pypx[t]{x} + \pypx[y]{z}\pypx[t]{y} $$

Example 14.5.3

Consider $z = x^3 + xy^2$, $x = r\cos(\theta)$, and $y = r\sin(\theta)$.

$$ \begin{align*} z &= \left(r\cos(\theta)\right)^3 + r\cos(\theta)\left(r\sin(\theta)\right)^2 \\ \\ &= r^3\cos^3(\theta) + r^3\cos(\theta)\sin^2(\theta) \\ \\ &= r^3\cos(\theta)\left(\cos^2(\theta) + \sin^2(\theta)\right) \\ \\ &= r^3\cos(\theta) \\ \\ \pypx{z} &= 3x^2 + y^2 \\ \\ \pypx[y]{z} &= 2xy \\ \\ \pypx[r]{z} &= \pypx{z}\pypx[r]{x} + \pypx[y]{z}\pypx[r]{y} \\ \\ &= \left(3x^2 + y^2\right)\cos(\theta) + \left(2xy\right)\sin(\theta) \\ \\ &= \left(3r^2\cos^2(\theta) + r^2\sin^2(\theta)\right)\cos(\theta) + \left(2r^2\cos(\theta)\sin(\theta)\right)\sin(\theta) \\ \\ &= \left(2r^2\cos^2(\theta) + r^2\cos^2(\theta) + r^2\sin^2(\theta)\right)\cos(\theta) + 2r^2\cos(\theta)\sin^2(\theta) \\ \\ &= 2r^2\cos^3(\theta) + r^2\cos(\theta) + 2r^2\cos(\theta)\sin^2(\theta) \\ \\ &= 2r^2\cos(\theta)\left(\cos^2(\theta) + \sin^2(\theta)\right) + r^2\cos(\theta) \\ \\ &= 2r^2\cos(\theta) + r^2\cos(\theta) \\ \\ &= 3r^2\cos(\theta) \\ \\ \pypx[\theta]{z} &= \pypx{z}\pypx[\theta]{x} + \pypx[y]{z}\pypx[\theta]{y} \\ \\ &= \left(3x^2 + y^2\right)\left(-r\sin(\theta)\right) + \left(2xy\right)r\cos(\theta) \\ \\ &= -r\left(3r^2\cos^2(\theta) + r^2\sin^2(\theta)\right)\sin(\theta) + 2r^3\cos^2(\theta)\sin(\theta) \\ \\ &= -r^3\left(2\cos^2(\theta) + \cos^2(\theta) + \sin^2(\theta)\right)\sin(\theta) + 2r^3\cos^2(\theta)\sin(\theta) \\ \\ &= -r^3\left(2\cos^2(\theta)\sin(\theta) + \sin(\theta)\right) + 2r^3\cos^2(\theta)\sin(\theta) \\ \\ &= -2r^3\cos^2(\theta)\sin(\theta) - r^3\sin(\theta) + 2r^3\cos^2(\theta)\sin(\theta) \\ \\ &= -r^3\sin(\theta) \end{align*} $$

In this example the partial derivatives $\pypx[r]{z}$ and $\pypx[\theta]{z}$ can be easily checked using $z(r,\theta)$ above.

Exercise 14.5.2

Consider the function $z = x^2y^3$, where $x = s+t$ and $y = s-t$. Compute $\pypx[s]{z}$ and $\pypx[t]{z}$.

Check your work

$$ \begin{align*} \pypx[s]{z} &= \pypx{z}\pypx[s]{x} + \pypx[y]{z}\pypx[s]{y} \\ \\ &= \left(2xy^3\right)\left(1\right) + \left(3x^2y^2\right)(1) \\ \\ &= 2(s+t)(s-t)^3 + 3(s+t)^2(s-t)^2 \\ \\ &= (s+t)(s-t)^2\left(2(s-t) + 3(s+t)\right) \\ \\ &= (s+t)(s-t)^2(5s+t) \\ \\ \\ \pypx[t]{z} &= \pypx{z}\pypx[t]{x} + \pypx[y]{z}\pypx[t]{y} \\ \\ &= \left(2xy^3\right)\left(1\right) + \left(3x^2y^2\right)(-1) \\ \\ &= xy^2(2y - 3x) \\ \\ &= (s+t)(s-t)^2\left(2(s-t) - 3(s+t)\right) \\ \\ &= (s+t)(s-t)^2(5s-5t) \\ \\ &= 5(s+t)(s-t)^3 \end{align*} $$

14.5.8 The General Chain Rule

Theorem 14.5.4

The General Chain Rule
Suppose that $u$ is a differentiable function of $n$ variables $x_j$,

$$ u = u(x_1, x_2, \dots, x_n) $$
and each $x_j$ is a function of $m$ variables $t_k$,

$$ x_j = x_j(t_1, t_2, \dots, t_m) $$
Then the $m$ first order partial derivatives of $u$ with respect to each $t_k$ is given by

$$ \pypx[t_k]{u} = \pypx[x_1]{u}\pypx[t_k]{x_1} + \pypx[x_2]{u}\pypx[t_k]{x_2} + \dots + \pypx[x_n]{u}\pypx[t_k]{x_n} $$
for $k=1,2,\dots,m$.

Example 14.5.4

Write out the chain rule for the case where $z = f(x,y)$ and $x = x(u,v,w)$, and $y = y(u,v,w)$. We will apply Theorem 4 using $n=2$ and $m=3$.

$$ \begin{align*} \pypx[u]{z} &= \pypx{z}\pypx[u]{x} + \pypx[y]{z}\pypx[u]{y} \\ \\ \pypx[v]{z} &= \pypx{z}\pypx[v]{x} + \pypx[y]{z}\pypx[v]{y} \\ \\ \pypx[w]{z} &= \pypx{z}\pypx[w]{x} + \pypx[y]{z}\pypx[w]{y} \\ \end{align*} $$

Example 14.5.5

Consider the function $z = x^2y^2$, where $x = r^2 + s^2$ and $y = 2rs$. Compute the second partial derivative of $z$ with respect to $r$.

$$ \begin{align*} \pypx[r]{z} &= \pypx{z}\pypx[r]{x} + \pypx[y]{z}\pypx[r]{y} \\ \\ &= \left(2xy^2\right)\left(2r\right) + \left(2x^2y\right)\left(2s\right) \\ \\ &= 4r\left(r^2 + s^2\right)\left(2rs\right)^2 + 4s\left(r^2 + s^2\right)^2\left(2rs\right) \\ \\ &= 16r^3s^2\left(r^2 + s^2\right) + 8rs^2\left(r^2 + s^2\right)^2 \\ \\ &= 8rs^2\left(r^2 + s^2\right)\left(2r^2 + r^2 + s^2 \right) \\ \\ &= 8rs^2\left(r^2 + s^2\right)\left(3r^2 + s^2\right) \\ \\ \\ \dfrac{\partial^2 z}{\partial r^2} &= \pypx[r]{}\left(\pypx[r]{z}\right) = \pypx[r]{} \left(\pypx{z}\pypx[r]{x} + \pypx[y]{z}\pypx[r]{y} \right) \\ \\ &= \dfrac{\partial}{\partial r}\left[8rs^2\left(r^2 + s^2\right)\left(3r^2 + s^2\right)\right] \\ \\ &= 8s^2\left(r^2 + s^2\right)\left(3r^2 + s^2\right) + 16r^2s^2\left(3r^2 + s^2\right) + 48r^2s^2\left(r^2 + s^2\right) \\ \\ &= 8s^2\left(r^2 + s^2\right)\left(3r^2 + s^2\right) + 96r^4s^2 + 64r^2s^4 \\ \\ &= 8s^2\left(r^2 + s^2\right)\left(3r^2 + s^2\right) + 32r^2s^2\left(3r^2 + 2s^2\right) \end{align*} $$

14.5.9 Implicit Differentiation

We are now in a position to more naturally explain implicit differentiation. Suppose that we have a function of two variables,

$$ z = F(x,y) $$
and we consider the level set $F(x,y) = k$ for some real number $k$. This gives us an equation that implicitly defines $y$ as a function of $x$, $F(x,f(x)) = k$. The chain rule tells us that

$$ \pypx{z} = \pypx{F}\dydx{x} + \pypx[y]{F}\dydx{y} = 0 $$
since the derivative of a constant with respect to $x$ is zero. Clearly $\dydx{x}=1$. Thus if $\pypx[y]{F}\neq 0$ we have the following theorem.

Theorem 14.5.5

Implicit Differentiation
Suppose that $z = F(x,y)$ is a differentiable function of two variables on a disk containing the point $(a,b)$ so that both $F_x$ and $F_y$ are continuous, and $\dfrac{\partial F}{\partial y}\neq 0$ on this disk. Then the level set $F(x,y)=k$ implicitly defines a function $y=f(x)$ so that $F(x,f(x))=k$ and at the point $(a,b)$ this implicit function is differentiable with

$$ \dydx{y} = -\dfrac{\pypx{F}}{\pypx[y]{F}} = -\dfrac{F_x}{F_y} $$

Notice that the first order partials $F_x$ and $F_y$ must both be continuous and $F_y\neq 0$ on a disk containing the point $(a,b)$ where $F$ is differentiable. If the implicit function $F(x,y)=k$ is implicitly differentiable at every point in the interior of the disk, then we say that the implicit function is differentiable on the disk .

We can use these same conditions to implicitly compute partial derivatives.

Theorem 14.5.6

The Implicit Function Theorem
If $z = F(x_1, x_2, \dots, x_n)$ is a differentiable function of $n$ variables inside an $n$-sphere containing point $(a_1, a_2, \dots, a_n)$, and all $n$ partial derivatives $\pypx[x_1]{F}$, $\pypx[x_2]{F}$, $\dots$, $\pypx[x_n]{F}$ are continuous and $\pypx[x_k]{F}\neq 0$ inside this sphere; then the level set $F(x_1, x_2, \dots, x_n) = 0$ defines an implicit function of $x_k$ in terms of the other $n-1$ variables and

$$ \pypx[x_j]{x_k} = -\dfrac{\pypx[x_k]{F}}{\pypx[x_j]{F}} = -\dfrac{F_{x_k}}{F_{x_j}} $$
for all $1\le k\neq j\le n$.

Example 14.5.6

Consider the equation $w = F(x,y,z) = x^3 + y^3 + z^3 - 6xyz = 1$. Find $\pypx[x]{z}$ and $\pypx[y]{z}$.

The equation $x^3 = y^3 + z^3 - 6xyz = 1$ defines a three dimensional surface in $\mathbb{R}^4$.

$$ \begin{align*} \pypx{F} &= \pypx{w} = 3x^2 - 6yz \\ \\ \pypx[y]{F} &= \pypx[y]{w} = 3y^2 - 6xz \\ \\ \pypx[z]{F} &= \pypx[z]{w} = 3z^2 - 6xy \end{align*} $$
$F_x$, $F_y$, and $F_z$ are all continuous on all of $\mathbb{R}^3$ since they are polynomials. If $F_z=0$, then

$$ \begin{align*} 0 &= 3z^2 - 6xy \\ 0 &= z^2 - 2xy \\ z^2 &= 2xy \\ \end{align*} $$

The graph of $z^2 = 2xy$
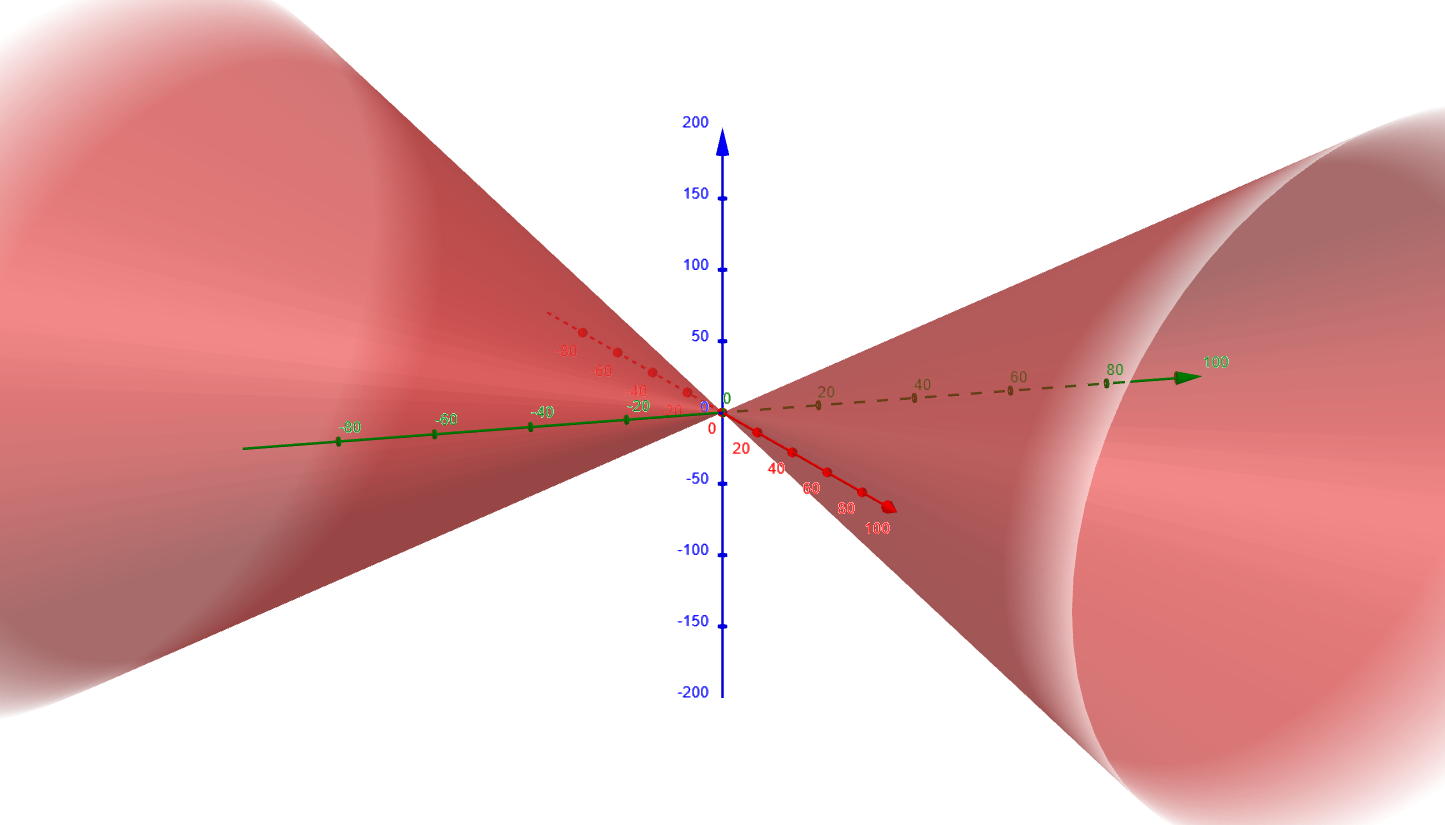
Figure 2

For any points not on the surface $z^2=2xy$, the equation $x^3 + y^3 + z^3 - 6xy - 1 = 0$ implicitly defines $z$ as a function of $x$ and $y$ such that

$$ \begin{align*} \pypx{z} &= -\dfrac{F_x}{F_z} = -\dfrac{3x^2-6yz}{3z^2-6xy} = -\dfrac{x^2-2yz}{z^2-2xy} \\ \\ \pypx[y]{z} &= -\dfrac{F_y}{F_z} = -\dfrac{3y^2-6xz}{3z^2-6xy} = -\frac{y^2-2xz}{z^2-2xy} \end{align*} $$

Your use of this self-initiated mediated course material is subject to our Creative Commons License .

Creative Commons Attribution-NonCommercial-ShareAlike 4.0


Attribution
You must give appropriate credit, provide a link to the license, and indicate if changes were made. You may do so in any reasonable manner, but not in any way that suggests the licensor endorses you or your use.


Noncommercial
You may not use the material for commercial purposes.


Share Alike
You are free to share, copy and redistribute the material in any medium or format. If you adapt, remix, transform, or build upon the material, you must distribute your contributions under the same license as the original.