Math 344: Calculus III
14.7 Maximum and Minimum Values
14.7.1 Extrema for Function with One Output ¶
If a function $ \def\ihat{\mathbf{\hat{\mmlToken{mi}[mathvariant="bold"]{ı}}}} \def\jhat{\mathbf{\hat{\mmlToken{mi}[mathvariant="bold"]{ȷ}}}} \def\khat{\mathbf{\hat{k}}} \newcommand{\pypx}[2][x]{\dfrac{\partial #2}{\partial #1}} \newcommand{\dydx}[2][x]{\dfrac{d #2}{d #1}} \newcommand{\deltax}[2][x]{\frac{\Delta #2}{\Delta #1}} f:\mathbb{R}^n\rightarrow\mathbb{R} $ has only one output then naturally we want to know if the output has any maximum or minimum values. For example, the paraboloid $z = x^2 + y^2$ has an absolute minimum at the origin of the graph.
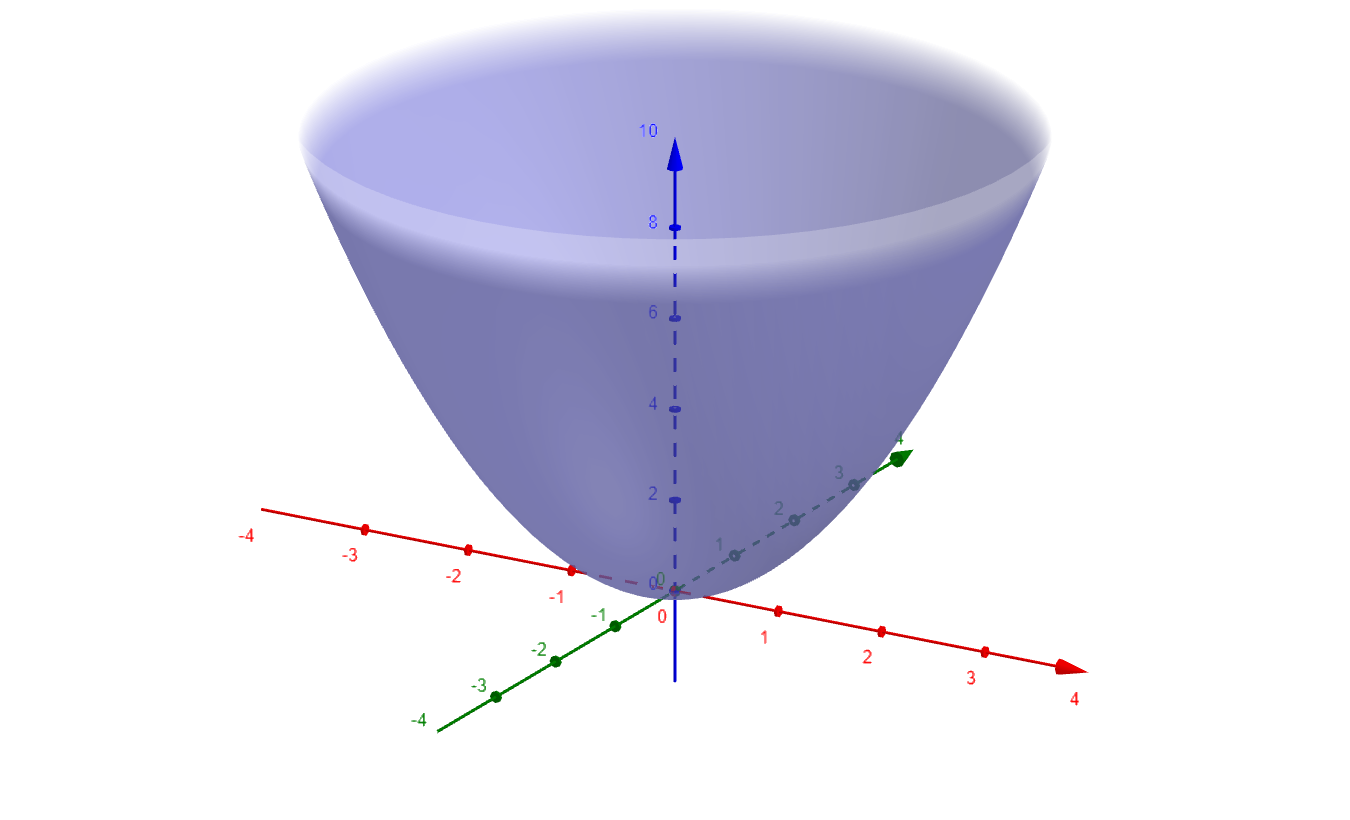
Figure 1
Definition ¶
Local Extrema
A function of two variables has a local minimum at $(a,b)$ if there is a disk $D$ of radius $r\gt 0$ centered at the point $(a,b)$ in the domain such that $f(x,y)\ge f(a,b)$ at every point $(x,y)\in D$.A function of two variables has a local maximum at $(a,b)$ if there is a disk $D$ of radius $r\gt 0$ centered at the point $(a,b)$ in the domain such that $f(x,y)\le f(a,b)$ at every point $(x,y)\in D$.
For any disk of radius $r>0$ centered at $(0,0)$ the value of $f(x,y)\ge 0 = f(0,0)$ in our paraboloid. Hence $(0,0)$ is a local minimum for our function $f$.
Definition ¶
Absolute Extrema
A function of two variables has an absolute minimum at $(a,b)$ if $f(x,y)\ge f(a,b)$ for every element $(x,y)$ in the domain.A function of two variables has an absolute maximum at $(a,b)$ if $f(x,y)\le f(a,b)$ for every element $(x,y)$ in the domain.
Our paraboloid has an absolute minimum at the point $(0,0)$. A extremum or extreme point is a minimum or maximum.
Theorem ¶
If a function of two variables $f$ has a local extremum at point $(a,b)$ and both first order partial derivatives $f_1$ and $f_2$ exist at $(a,b)$, then $f_1(a,b) = f_2(a,b)=0$.
Proof ¶
If $f:D\subset\mathbb{R}^2\rightarrow\mathbb{R}$, then define $D_x$ to be the intersection of our domain $D$ with the $x$-axis, and $g:D_x\rightarrow\mathbb{R}$ by $g(x)=f(x,b)$. Then $g$ has an extremum at $x=a$ and $g'(a)=f_x(a,b)$. Since $g$ is differentiable at $x=a$ and $g$ has an extreme value at $x=a$, $g'(a)=0$ from Calculus I. Hence $f_x(a,b) = g'(a) = 0$. Similarly $f_y(a,b)=0$.
If we use our values for $f_x(a,b)$ and $f_y(a,b)$ in the equation of the tangent plane, we have that the equation of the tangent plane is
$$
z = z_0 + f_x(a,b)(x-a) + f_y(a,b)(y-b) = z_0
$$
This means that the tangent plane is parallel to the $xy$-plane. Geometrically this means that if such a function has an extreme value and a tangent plane at a point $(a,b)$, the tangent plane is horizontal at that point.
Definition ¶
A function of two variables for which $f_1(a,b) = f_2(a,b) = 0$ or one of these partial derivatives does not exist is called a critical point or stationary point .
Just as in function of one variable, not all critical points are extrema. A critical point of a function of two variable may be a maximum, minimum or neither.
Example 14.7.1 ¶
Consider $f(x,y) = x^4 + y^4 - 2x^2 + 4y^2 + 1$. Setting the two first order partial derivatives to zero yields
$$
\begin{align*}
f_x(x,y) = 4x^3 - 4x &= 0 &\qquad f_y(x,y) = 4y^3 + 8y &= 0\\
\\
4x(x^2-1) &= 0 &\qquad 4y(y^2+2) &= 0 \\
\\
4x(x-1)(x+1) &= 0 &\qquad 4y(y^2+2) &= 0 \\
\\
x &= 0,1,-1 &\qquad y &= 0 \\
\end{align*}
$$
Thus $(a,b)=(0,0)$, $(1,0)$ and $(-1,0)$ are critical points of $f$ with
$$
\begin{align*}
f(0,0) &= 1 \\
f(1,0) &= 0 \\
f(-1,0) &= 0
\end{align*}
$$
Completing the square in the definition of $f$ gives us
$$
\begin{align*}
f(x,y) &= x^4 + y^4 - 2x^2 + 4y^2 + 1 \\
&= x^4 + y^4 - 2x^2 + 1 - 1 + y^4 + 4y^2 + 4 - 4 + 1 \\
&= \left(x^2 - 1\right)^2 + \left(y^2 + 2\right)^2 - 4
\end{align*}
$$
Though $x^2-1$ may be negative, $\left(x^2-1\right)^2 \ge 0$. Furthermore $y^2\ge 0$, so $y^2+2\ge 2$, and $\left(y^2 + 2\right)^2\ge 4$. Hence
$$
f(x,y) = \left(x^2 - 1\right)^2 + \left(y^2 + 2\right)^2 - 4 \ge 0 + 4 - 4 = 0
$$
Thus $(1,0,0)$ and $(-1,0,0)$ are absolute minimums. Graphically we can see that $(0,0,1)$ is neither a maximum nor a minimum. If we define functions
$$
\begin{align*}
g(x) &= f(x,0), &\ h(y) &= f(0,y) \\
\\
g''(x) &= 12x^2 - 4, &\ h''(y) &= 12y^3 + 8 \\
\\
g''(0) &= -4, &\ h''(0) &= 8
\end{align*}
$$
The level curve $z = f(x,0)$ is concave down, however the level curve $z = f(0,y)$ is concave up. The point $(0,0,1)$ is called a
saddle point
of $f$.

Figure 2
14.7.2 The Second Derivatives Test ¶
Definition ¶
The Second Derivatives Test
Suppose that all four second order partial derivatives of function $f:\mathbb{R}^2\rightarrow\mathbb{R}$ are continuous on a disk containing critical point $(a,b)$. That is $f_x(a,b) = f_y(a,b)=0$. Define $D$ by the determinant
$$ D(a,b) = \begin{vmatrix} f_{xx}(a,b) & f_{xy}(a,b) \\ f_{yx}(a,b) & f_{yy}(a,b) \end{vmatrix} = f_{xx}(a,b)f_{yy}(a,b) - \left[f_{xy}(a,b)\right]^2 $$
(a) If $D\gt 0$ and $f_xx(a,b)>0$ or $f_yy(a,b)>0$, then $f(a,b)$ is a local minimum
(b) If $D\gt 0$ and $f_xx(a,b)<0$ or $f_yy(a,b)<0$, then $f(a,b)$ is a local minimum
(c) If $D\lt 0$ then $f(a,b)$ is a saddle point
(d) If $D=0$, then the test is inconclusive
Example 14.7.2 ¶
Consider the surface $z = \frac{1}{3}x^3 + 2xy − 3x − y^2$
To find the critical points we set the first order partial derivatives to zero,
$$
\begin{align*}
z_x = x^2 + 2y - 3 &= 0 &\ z_y = 2x - 2y &= 0 \\
\\
y^2 + 2y - 3 &= 0 &\ 2x &= 2y \\
\\
(y+3)(y-1) &= 0 &\ x &= y \\
\\
y &= -3,1
\end{align*}
$$
The critical points are $(-3,-3)$ and $(1,1)$.
$$
\begin{align*}
D(x,y) &= \begin{vmatrix} f_{xx}(a,b) & f_{xy}(a,b) \\ f_{yx}(a,b) & f_{yy}(a,b) \end{vmatrix} = \begin{vmatrix} 2x + 2 & 2 \\ 2 & -2 \end{vmatrix} \\
\\
D(-3,-3) &= \begin{vmatrix} -6+2 & 2 \\ 2 & -2 \end{vmatrix} = (-4)(-2) - (2)(2) = 8 - 4 = 4 > 0 \\
f_{xx}(-3,-3) &= -4 < 0 \\
\\
D(1,1) &= \begin{vmatrix} 2 + 2 & 2 \\ 2 & -2 \end{vmatrix} = (4)(-2) - (2)(2) = -8 - 4 = -12 < 0
\end{align*}
$$
Thus $(-3,-3,9)$ is a local maximum and $\left(1,1,-\frac{5}{3}\right)$ is a saddle point.
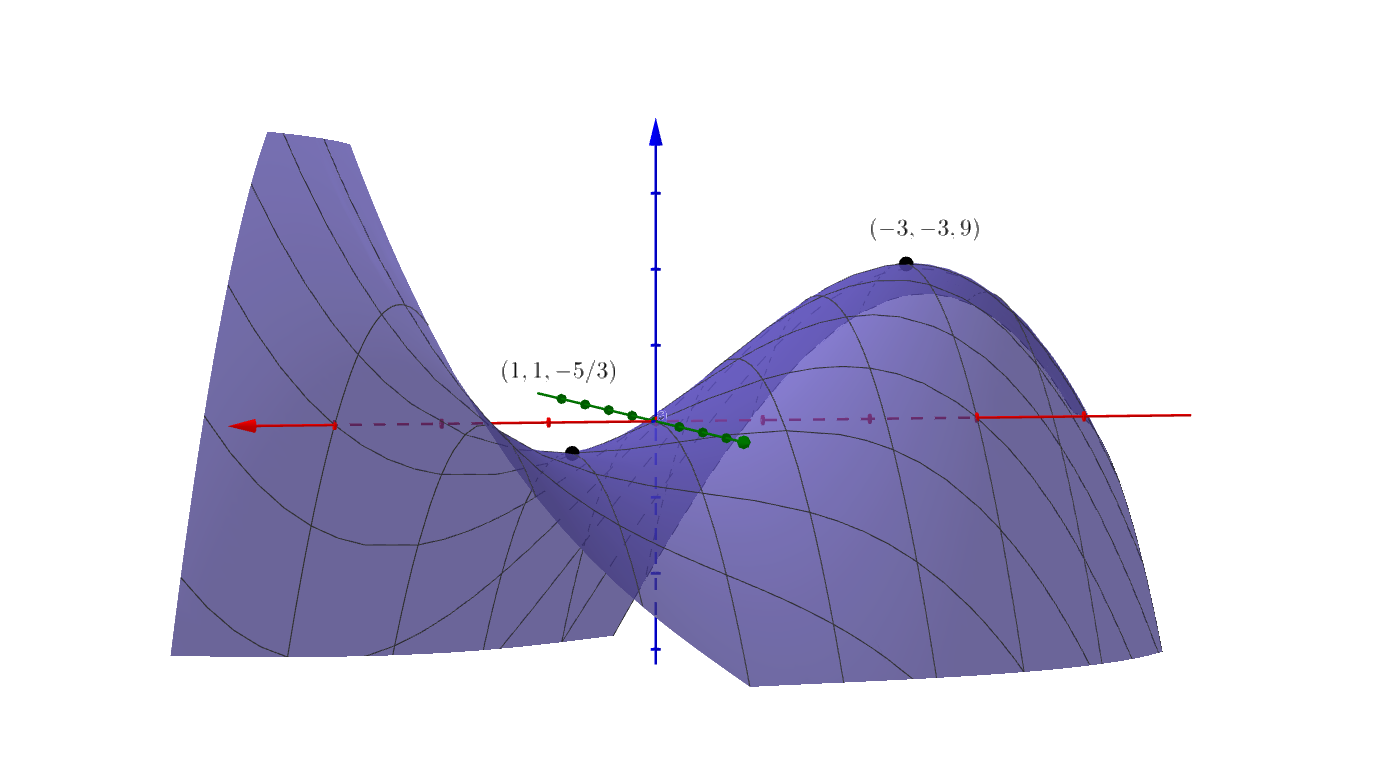
Figure 3
14.7.3 Absolute Extrema ¶
A
closed
subset of $\mathbb{R}^2$ is a set that contains all of its boundary points. An
open
set is a set that contains none of its boundary points. A
LOT
of sets are neither open nor closed. A
closed ball
or
closed disk
in $\mathbb{R}^2$ of radius $r\gt 0$ centered at the point $(h,k)$ is defined
$$
\overline{D} = \left\{ (x,y)\in\mathbb{R}^2\,:\,(x-h)^2 + (y-k)^2 \le r^2 \right\}
$$
An
open ball
or
open disk
in $\mathbb{R}^2$ of radius $r\gt 0$ centered at the point $(h,k)$ is defined
$$
D = \left\{ (x,y)\in\mathbb{R}^2\,:\,(x-h)^2 + (y-k)^2 \lt r^2 \right\}
$$
The points on the circle, $x^2 + y^2 = r^2$ are
boundary points
of both sets.
A bounded set is a set that is entirely contained inside of an open disk centered at the origin. Some bounded sets may need a disk with a VERY big radius to contain it! The rectangle $[5280,6000]\times[-1,1]$ is far from the origin, but contained in the disk of radius 12,000 centered at the origin.
Theorem ¶
The Extreme Value Theorem for Function of Two Variables
If $f$ is continuous on a closed bounded set $D$ in $\mathbb{R}^2$, then $f$ attains an absolute maximum value $f(x_1,y_1)$ and an absolute minimum value $f(x_2,y_2)$ at some points $(x_1,y_1)$ and $(x_2,y_2)$ in $D$.
Finding the absolute extrema of a function on a closed bounded set $D\subset\mathbb{R}^2$ requires several steps.
-
Find the values of $f$ at the critical points that are in the domain $D$. This requires finding the points where the tangent plane is horizontal, or one of the first order partials does not exist in the domain $D$.
-
Find the extrema of the boundary points. This usually requires methods from Calculus I.
-
The largest and smallest values of $f$ in steps one and two are the absolute extreme values.
Example 14.7.3 ¶
Consider the surface $g(x,y) = x^2 + y^2 + 4x − 6y$ on the domain defined by $D = \left\{ (x,y)\,:\,x^2 + y^2 \le 16 \right\}$.
$$
\begin{align*}
g_x = 2x + 4 &= 0 &\ g_y = 2y - 6 &= 0 \\
\\
2x &= -4 &\ 2y &= 6 \\
\\
x &= -2 &\ y &= 3 \\
\end{align*}
$$
The point $(-2,3)$ is the only critical point in the open interior of the disk. On the boundary circle of the disk we can parameterize the curve by $z = \left(4\cos(\theta), 4\sin(\theta)\right)$ on the interval $[0,2\pi]$. Thus the value of our function on the boundary
$$
\begin{align*}
z(\theta) &= 16\cos^2(\theta) + 16\sin^2(\theta) + 16\cos(\theta) - 24\sin(\theta) \\
\\
&= 16 + 16\cos(\theta) - 24\sin(\theta)
\\
z'(\theta) &= -16\sin(\theta) - 24\cos(\theta) = 0 \\
\\
24\cos(\theta) &= -16\sin(\theta) \\
\\
\tan(\theta) = \dfrac{\sin(\theta)}{\cos(\theta)} &= -\frac{24}{16} = -\dfrac{3}{2} \\
\\
\theta &= \tan^{-1}\left(-\frac{3}{2}\right), \tan^{-1}\left(-\frac{3}{2}\right) + \pi
\end{align*}
$$
The values of our function at are approximately
$$
\begin{align*}
f(-2,3) &= -13) \\
f\left(4\cos(\theta), 4\sin(\theta)\right) &\approx 44.84 \\
f\left(-4\cos(\theta),-4\sin(\theta)\right) &\approx -12.84
\end{align*}
$$
Thus the absolute maximum at $\left(4\cos(\theta), 4\sin(\theta)\right)$ and the absolute minimum occurs at $(-2,3)$.
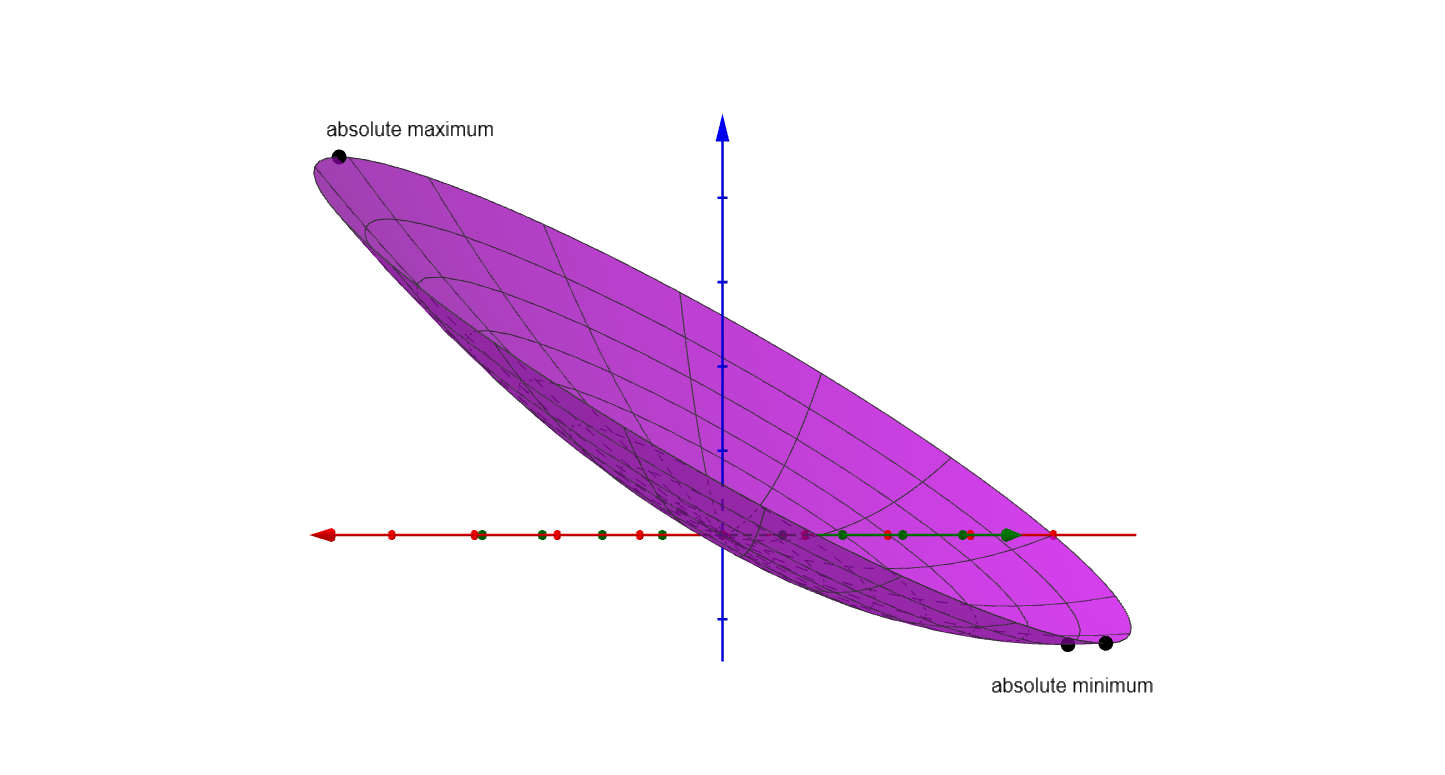
Figure 4
Exercise 14.7.1 ¶
Find the absolute minimum and maximum values of the function
$$ f(x,y) = x^2 + xy + y^2 - 6y $$
on the set
$$ D = \left\{(x,y) : x\in [-3,3],\ y\in [0,5]\right\} $$
Check Your Work
Minimum: $f\left(-2,4\right) = -12$. Maximum: $f\left(3,5\right) = 19$.Video Solution

Your use of this self-initiated mediated course material is subject to our Creative Commons License .
Creative Commons Attribution-NonCommercial-ShareAlike 4.0

Attribution
You must give appropriate credit, provide a link to the license, and indicate if changes were made. You may do so in any reasonable manner, but not in any way that suggests the licensor endorses you or your use.

Noncommercial
You may not use the material for commercial purposes.

Share Alike
You are free to share, copy and redistribute the material in any medium or format. If you adapt, remix, transform, or build upon the material, you must distribute your contributions under the
same license
as the original.