Math 344: Calculus III

15.1 Double Integrals Over Rectangles

---

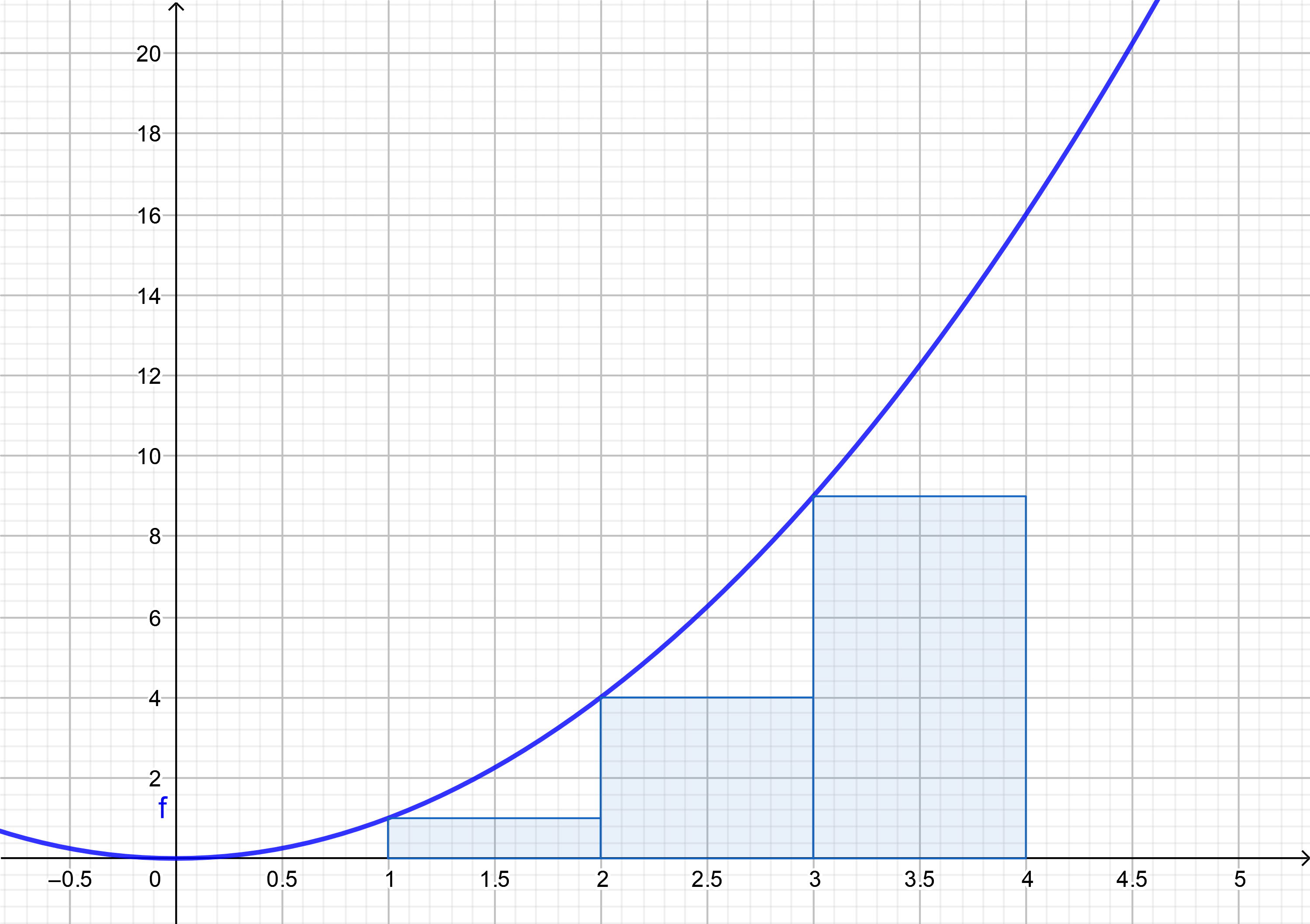
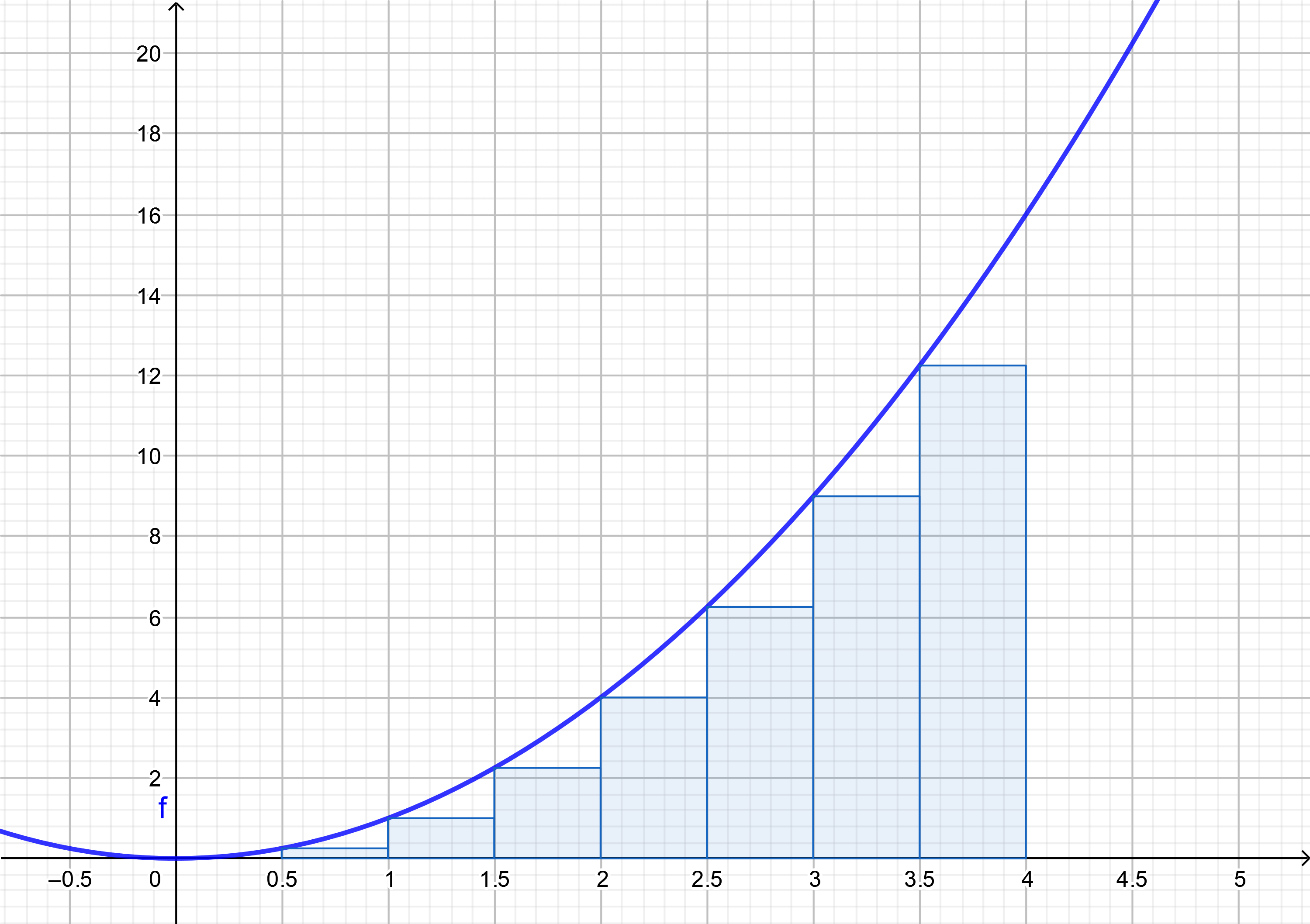
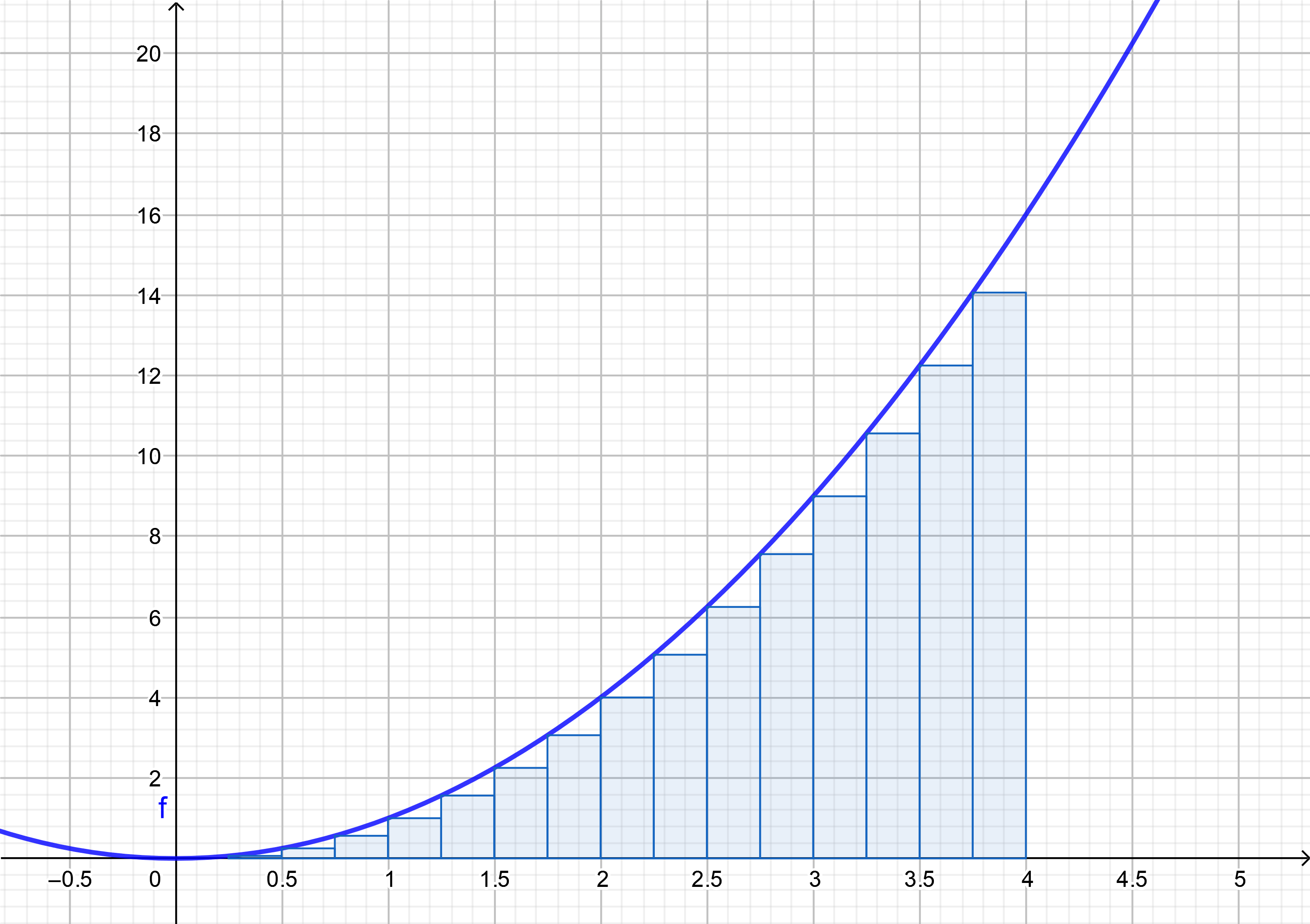
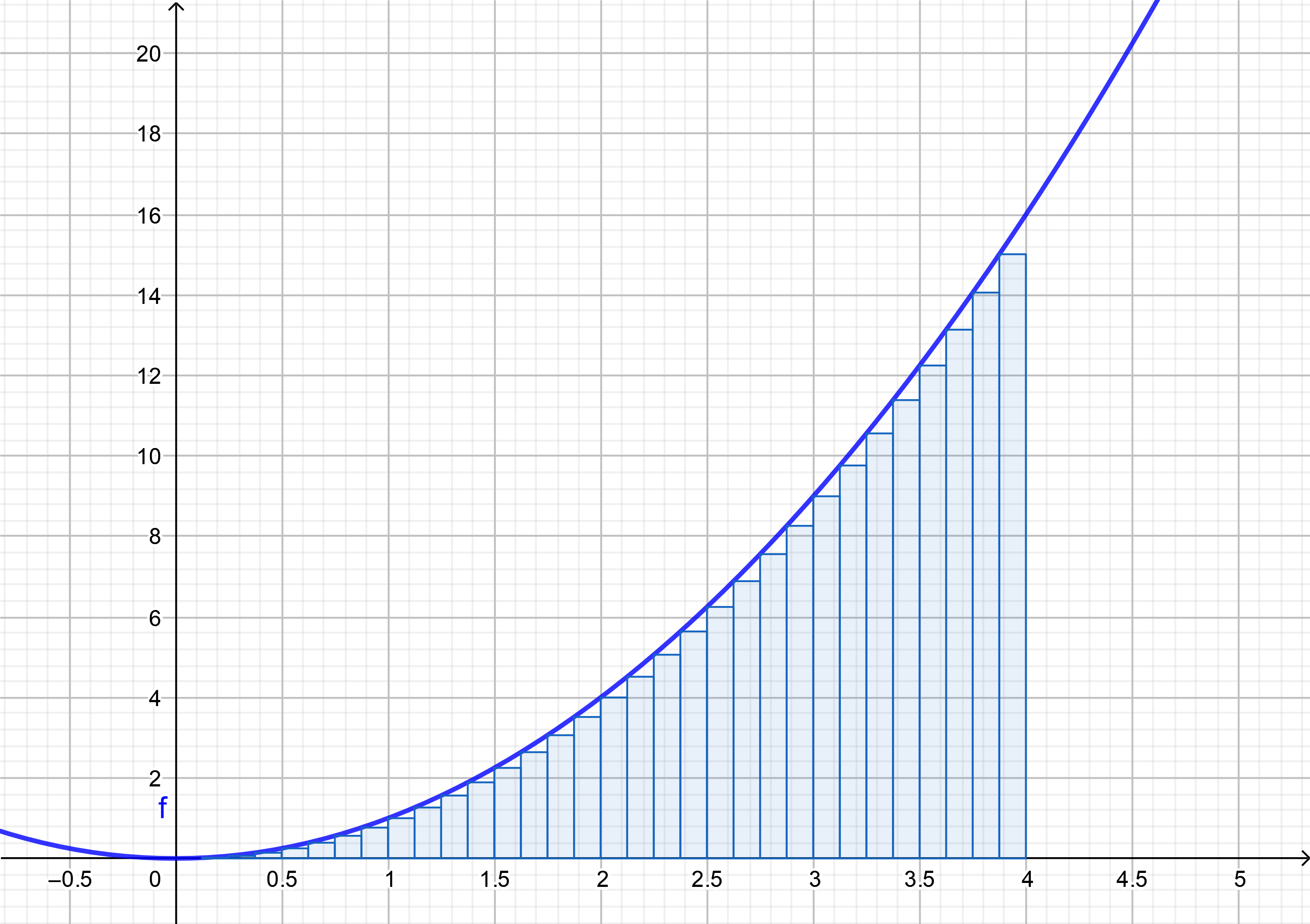
15.1.1 Review the Definite Integral

The Definite integral from our first semester of calculus is a limit of Riemann Sums .

Riemann sums for $ \require{color} \definecolor{brightblue}{rgb}{.267, .298, .812} \definecolor{darkblue}{rgb}{.08, .18, .28} \definecolor{palepink}{rgb}{1, .73, .8} \definecolor{softmagenta}{rgb}{.99,.34,.86} \def\ihat{\mathbf{\hat{\mmlToken{mi}[mathvariant="bold"]{ı}}}} \def\jhat{\mathbf{\hat{\mmlToken{mi}[mathvariant="bold"]{ȷ}}}} \def\khat{\mathbf{\hat{k}}} \newcommand{\pypx}[2][x]{\dfrac{\partial #2}{\partial #1}} \newcommand{\dydx}[2][x]{\dfrac{d #2}{d #1}} \newcommand{\deltax}[2][x]{\frac{\Delta #2}{\Delta #1}} y = x^2$ from $a=0$ to $b=4$

n = 4	n = 8
n = 16	n = 32

Figure 1

Each of these Riemann sums is a finite sum


$$ \text{Riemann Sum } = \displaystyle\sum_{k=1}^n f(x_k^{*})\,\Delta x = \displaystyle\sum_{k=1}^n f(x_k^{*})\dfrac{b-a}{n} $$
where $\Delta x = \dfrac{b-a}{n}$ is the length of each subinterval , and $x_k^{*}$ is an element of the subinterval $\left[ a+(k-1)\Delta x,\ a+k\Delta x\right]$.

If the limit of Riemann sums is a finite value, the we call the limit, integral of $f$ from $a$ to $b$ and interpret this value to be the area under the curve .

$$ \text{Area } = \displaystyle\lim_{n\rightarrow\infty}\displaystyle\sum_{k=1}^n f(x^{*})\Delta x = \displaystyle\int_a^b f(x)\,dx $$
Moreover the value of the definite integral can be easily computed using the Fundamental Theorem of Calculus . If $F$ is any antiderivative of $f$; that is $F'(t) = f(t)$, then

$$ \displaystyle\int_a^b f(x)\,dx = F(b) - F(a) $$

15.1.2 Double Riemann Sum Over a Rectangle

A rectangle in the $xy$-plane consists of all of the points with first coordinate $x$ in an interval $[a,b]$ and second coordinate $y$ in another interval $[c,d]$.

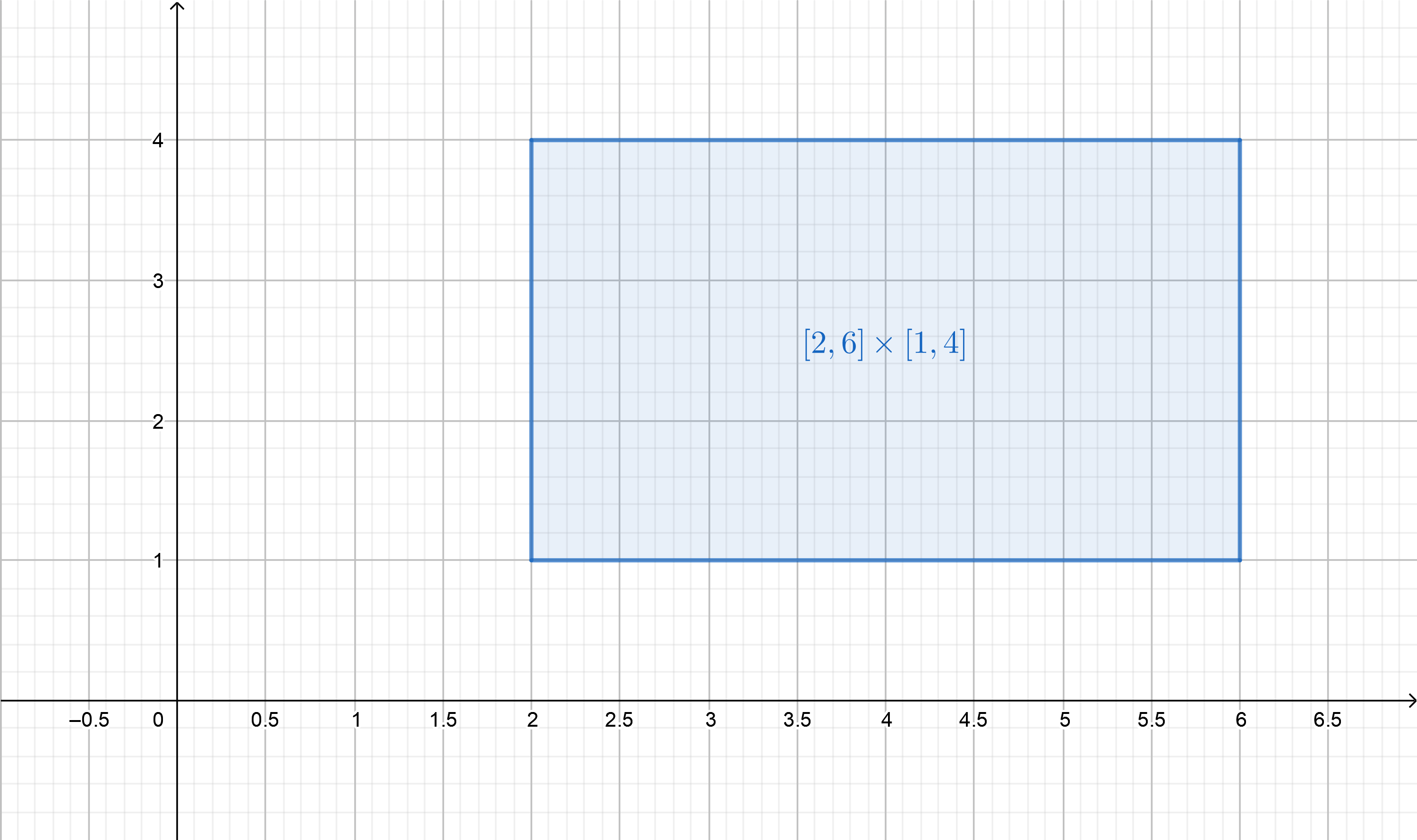Rectangular domain $[2,6]\times[1,4]$ in the $xy$-plane Figure 2

A function with two real inputs and one real output gives us a height $z$ for each input $(x,y)$

$$ z = f(x,y) $$
We can plot the height above (or below) the $xy$-plane in a three-dimensional coordinate system

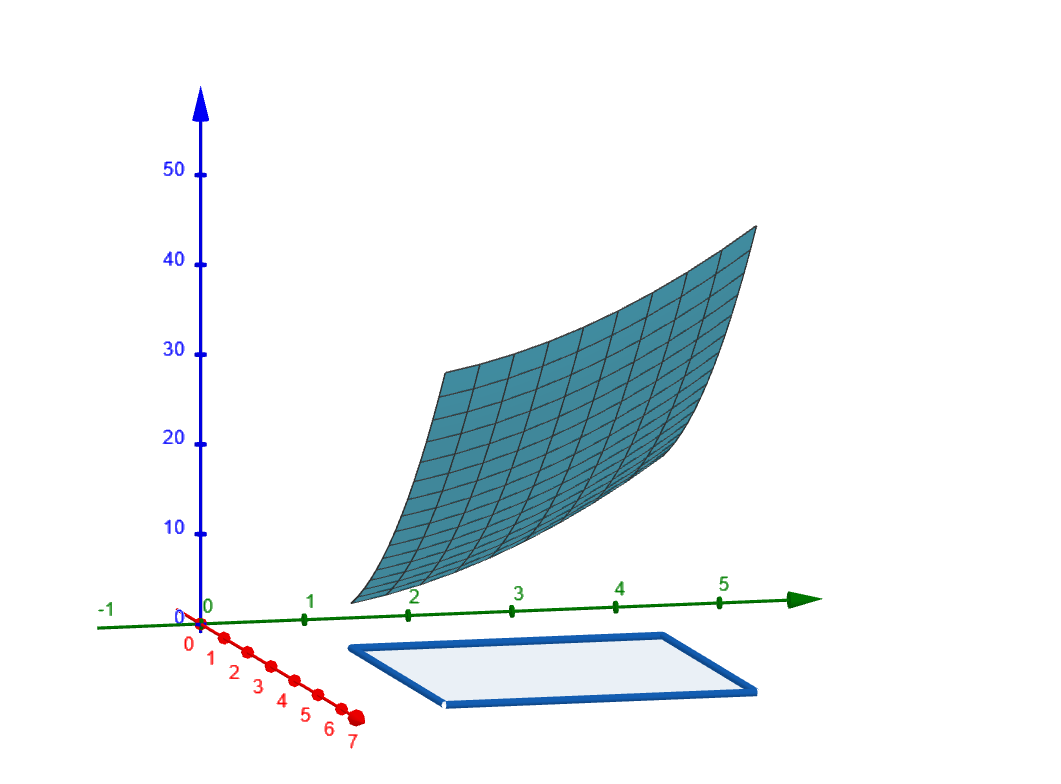Surface $z = x^2 + y^2$ over the Rectangle $[2,6]\times[1,4]$ Figure 3

A Riemann Sum over a rectangular domain is a double sum

$$ \text{Riemann Sum } = \displaystyle\sum_{i=1}^m\displaystyle\sum_{j=1}^n f(x_i^{*},y_j^{*})\Delta A = \displaystyle\sum_{i=1}^m\displaystyle\sum_{j=1}^n f(x_i^{*},y_j^{*})\Delta x\Delta y = \displaystyle\sum_{i=1}^m\displaystyle\sum_{j=1}^n f(x_i^{*},y_j^{*})\,\dfrac{(b-a)}{m}\,\dfrac{(d-c)}{n}, $$
where

• $\Delta x = \dfrac{b-a}{m}$ is the length of each subinterval on the $x$-axis,
  
  
• $\Delta y = \dfrac{d-c}{n}$ is the length of each subinterval on the $y$-axis,
  
  
• $x_i^{*}$ is an element of the subinterval $\left[ a+(i-1)\Delta x,\ a+i\Delta x\right] = I_i$,
  
  
• $y_j^{*}$ is an element of the subinterval $\left[ c+(j-1)\Delta y,\ a+j\Delta y\right] = I_j$
  
• $R_{ij} = I_i\times I_j$
  
  
• $\Delta A = \Delta x\Delta y = $ Area of $R_{ij}$.
  
  

This means that each point $(x_i^{*},y_j^{*})$ is an element of subrectangle

$$ R_{ij} := \left[ a+(i-1)\Delta x,\ a+i\Delta x\right]\times\left[ c+(j-1)\Delta y,\ a+j\Delta y\right]. $$

Riemann sums for $y = x^2 + y^2$ on the rectangle $[0,4]\times[0,4]$

$m\times n = 8\times 8$	$m\times n = 16\times 16$
$m\times n = 32\times 32$	$m\times n = 64\times 64$

Figure 4 (In these plots the $x$ and $y$-axes label the number of the rectangle; not the value in $[0,4]$.)

As in the case of a function of one real variable if the limit of Riemann double sums exists, then we call this limit the double integral of $f$ on rectangle $R$ and we interpret this value a the volume under the surface .

$$ \text{Volume } = \displaystyle\lim_{m\rightarrow\infty,\ n\rightarrow\infty}\displaystyle\sum_{i=1}^m\displaystyle\sum_{j=1}^n f(x_i^{*},y_j^{*})\Delta A = \displaystyle\iint_{R} f(x,y)\,dA $$

15.1.3 Computing Double Integrals

How does one compute a double integral? Can we use some version of the Fundamental Theorem of Calculus to simplify computations?

Since the area of each rectangle is the product of the lengths of each side

$$ \Delta A = \Delta x \cdot \Delta y $$
and multiplication distributes over addition we have that each of our Riemann sums

$$ \begin{align*} \text{Riemann Sum } &= \displaystyle\sum_{i=1}^m\displaystyle\sum_{j=1}^n f(x_i^{*},y_j^{*})\Delta A \\ \\ &= \displaystyle\sum_{i=1}^m\displaystyle\sum_{j=1}^n f(x_i^{*},y_j^{*})\Delta x\Delta y \\ \\ &= \displaystyle\sum_{i=1}^m\left(\displaystyle\sum_{j=1}^n f(x_i^{*},y_j^{*})\Delta y\right)\Delta x \\ \\ \end{align*} $$
We can try computing the limits separately

$$ \begin{align*} \text{Volume } &= \displaystyle\lim_{m\rightarrow\infty,\ n\rightarrow\infty}\displaystyle\sum_{i=1}^m\displaystyle\sum_{j=1}^n f(x_i^{*},y_j^{*})\Delta x\Delta y \\ \\ &= \displaystyle\lim_{m\rightarrow\infty}\displaystyle\sum_{i=1}^m\left(\displaystyle\lim_{n\rightarrow\infty}\displaystyle\sum_{j=1}^n f(x_i^{*},y_j^{*})\Delta y\right)\Delta x \\ \\ &= \displaystyle\lim_{m\rightarrow\infty}\displaystyle\sum_{i=1}^m\left(\displaystyle\displaystyle\int_c^d f(x_i^{*},y)\,dy\right)\Delta x \\ \\ \end{align*} $$

$m\times n = 8\times 8$	$m\times n = 8\times 16$
$m\times n = 8\times 32$	$m\times n = 8\times 64$

Figure 5 (In these plots the $x$ and $y$-axes label the number of the rectangle; not the value in $[0,4]$.)

For any fixed but arbitrary $x\in[a,b]$, we have a map from $[a,b]\rightarrow\mathbb{R}$ defined by

$$ F(x) := \displaystyle\int_c^d f(x,y)\,dy $$ Figure 6 (The curves $f(0,y)$, $f(2,y)$ and $f(4,y)$)

$F(x_0)$ is the area under the level curve $f(x_0,y)$. In Figure 6

$$ \begin{align*} F(0) &= \displaystyle\int_0^4 f(0,y)\,dy = \displaystyle\int_0^4 0^2 + y^2\,dy = \left[ \dfrac{y^3}{3}\right]_0^4 = \dfrac{64}{3} \\ \\ F(2) &= \displaystyle\int_0^4 f(2,y)\,dy = \displaystyle\int_0^4 2^2 + y^2\,dy = \left[ \dfrac{4y + y^3}{3}\right]_0^4 = 16 + \dfrac{64}{3} = \dfrac{112}{3} \\ \\ F(4) &= \displaystyle\int_0^4 f(4,y)\,dy = \displaystyle\int_0^4 4^2 + y^2\,dy = \left[ \dfrac{16y + y^3}{3}\right]_0^4 = 64 + \dfrac{64}{3} = \dfrac{256}{3} \\ \end{align*} $$

We integrate a function of more than one variable just as differentiating a function of more than one real variable. When we integrate with respect to one variable, we consider the other variable(s) to be constant(s). We can use our previous experience to compute the antiderivative of the integrand with respect to $y$. If $G(x,y)$ is any function whose partial derivative $\dfrac{\partial G}{\partial y} = f(x,y)$, then

$$ F(x) = \displaystyle\int_c^d f(x,y)\,dy = G(x,d) - G(x,c) $$
Thus

$$ \begin{align*} \text{Volume } &= \displaystyle\lim_{m\rightarrow\infty}\displaystyle\sum_{i=1}^m\left(\displaystyle\displaystyle\int_c^d f(x_i^{*},y)\,dy\right)\Delta x \\ \\ &= \displaystyle\lim_{m\rightarrow\infty}\displaystyle\sum_{i=1}^m F(x_i^{*})\Delta x = \displaystyle\int_a^b F(x)\,dx \\ \\ &= \displaystyle\int_a^b \left(\displaystyle\displaystyle\int_c^d f(x,y)\,dy\right)\,dx = \displaystyle\int_a^b \displaystyle\displaystyle\int_c^d f(x,y)\,dy\,dx \\ \end{align*} $$
In our example we obtain

$$ \begin{align*} \displaystyle\int_a^b \displaystyle\displaystyle\int_c^d f(x,y)\,dy\,dx &= \displaystyle\int_0^4 \displaystyle\displaystyle\int_0^4 x^2+y^2\,dy\,dx \\ \\ &= \displaystyle\int_0^4 \left[ \displaystyle\displaystyle\int_0^4 x^2+y^2\,dy \right]\,dx \\ \\ &= \displaystyle\int_0^4 \left[ x^2y + \dfrac{y^3}{3} \right]_0^4\,dx \\ \\ &= \displaystyle\int_0^4 \left[ 4x^2 + \dfrac{64}{3} - \left(0x^2 + 0\right)\right]\,dx \\ \\ &= \displaystyle\int_0^4 4x^2 + \dfrac{64}{3}\, dx = \left[ \dfrac{4x^3}{3} + \dfrac{64}{3}x \right]_0^4 \\ \\ &= \dfrac{256}{3} + \dfrac{256}{3} - (0 + 0) = \dfrac{512}{3} \\ \end{align*} $$
This integral is called an iterated integral because one computes two real-valued integrals to evaluate it. Likewise we might distribute $\Delta y$ and compute the limit with respect to $x$ first to obtain another iterated integral.

$$ \begin{align*} \text{Volume } &= \displaystyle\lim_{m\rightarrow\infty,\ n\rightarrow\infty}\displaystyle\sum_{i=1}^m\displaystyle\sum_{j=1}^n f(x_i^{*},y_j^{*})\Delta x\Delta y \\ \\ &= \displaystyle\lim_{n\rightarrow\infty}\displaystyle\sum_{j=1}^n\left(\displaystyle\lim_{m\rightarrow\infty}\displaystyle\sum_{i=1}^m f(x_i^{*},y_j^{*})\Delta x\right)\Delta y \\ \\ &= \displaystyle\lim_{n\rightarrow\infty}\displaystyle\sum_{j=1}^n\left(\displaystyle\displaystyle\int_a^b f(x,y_j^{*})\,dx\right)\Delta y \\ \\ &= \displaystyle\int_c^d \displaystyle\displaystyle\int_a^b f(x,y)\,dx\,dy \\ \end{align*} $$
Returning to our example we obtain

$$ \begin{align*} \displaystyle\int_c^d \displaystyle\displaystyle\int_a^b f(x,y)\,dx\,dy &= \displaystyle\int_0^4 \displaystyle\displaystyle\int_0^4 x^2+y^2\,dx\,dy \\ \\ &= \displaystyle\int_0^4 \left[ \displaystyle\displaystyle\int_0^4 x^2+y^2\,dy \right]\,dy \\ \\ &= \displaystyle\int_0^4 \left[ \dfrac{x^3}{3} + xy^2 \right]_0^4\,dy \\ \\ &= \displaystyle\int_0^4 \dfrac{64}{3} + 4y^2 \,dy \\ \\ &= \left[ \dfrac{64}{3}y + \dfrac{4y^3}{3} \right]_0^4 = \dfrac{256}{3} + \dfrac{256}{3} = \dfrac{512}{3} \\ \end{align*} $$
This gives us three possible values for the double integral based upon what order and how we compute our limit of the Riemann sums

$$ \begin{align*} \displaystyle\iint_{R} f(x,y)\,dA &= \displaystyle\lim_{m\rightarrow\infty,\ n\rightarrow\infty}\displaystyle\sum_{i=1}^m\displaystyle\sum_{j=1}^n f(x_i^{*},y_j^{*})\Delta A \\ \\ \qquad\displaystyle\int_a^b \displaystyle\displaystyle\int_c^d f(x,y)\,dy\,dx &= \displaystyle\lim_{m\rightarrow\infty}\displaystyle\sum_{i=1}^m\left(\displaystyle\lim_{n\rightarrow\infty}\displaystyle\sum_{j=1}^n f(x_i^{*},y_j^{*})\Delta y\right)\Delta x \\ \\ \displaystyle\int_c^d \displaystyle\displaystyle\int_a^b f(x,y)\,dx\,dy &= \displaystyle\lim_{n\rightarrow\infty}\displaystyle\sum_{j=1}^n\left(\displaystyle\lim_{m\rightarrow\infty}\displaystyle\sum_{i=1}^m f(x_i^{*},y_j^{*})\Delta x\right)\Delta y \\ \end{align*} $$

15.1.4 Fubini's Theorem

Fubini's Theorem

If $f$ is continuous on a rectangle $R = \left\{(x,y)\,:\,a\le b,\ c\le d\right\}$, and any of the limits

$$ \displaystyle\iint_{R} f(x,y)\,dA,\qquad\qquad\displaystyle\int_a^b \displaystyle\displaystyle\int_c^d f(x,y)\,dy\,dx,\qquad\displaystyle\int_c^d \displaystyle\displaystyle\int_a^b f(x,y)\,dx\,dy $$
exist, then they are all equal.

The result of Fubini's theorem is that one chooses which of the three integrals appears the easiest to compute. If any one of them yields a finite value, then all three are equal.

15.1.5 Examples

Example 1

Let region $R = [0,1]\times[2,3]$ and compute $\displaystyle\int_R(xy+1)\,dA$.

Computing an iterated integral one obtains

$$ \begin{align*} \displaystyle\int_R(xy+1)\,dA &= \displaystyle\int_0^1\left[\int_2^3 (xy + 1)\,dy\right]dx \\ \\ &= \displaystyle\int_0^1\left[ \dfrac{xy^2}{2} + y\,\right]_2^3 dx \\ \\ &= \displaystyle\int_0^1\left[ \dfrac{9x}{2} + 3 - \left(\dfrac{4x}{2} + 2\right)\right]dx \\ \\ &= \displaystyle\int_0^1 \left(\dfrac{5}{2}x + 1\right)dx \\ \\ &= \left[ \dfrac{5}{4}x^2 + x \right]_0^1 = \dfrac{5}{4} + 1 - (0 + 0) = \dfrac{9}{4} \end{align*} $$
Just to check our work the other iterated integral yields

$$ \begin{align*} \displaystyle\int_R(xy+1)\,dA &= \displaystyle\int_2^3\left[\int_0^1 (xy + 1)\,dx\right]dy \\ \\ &= \displaystyle\int_2^3\left[ \dfrac{x^2y}{2} + x \right]_0^1dy \\ \\ &= \displaystyle\int_2^3\left[ \dfrac{y}{2} + 1 - (0 + 0)\right]dy \\ \\ &= \left[\dfrac{y^2}{4} + y\right]_2^3 = \dfrac{9}{4} + 3 - \left(\dfrac{4}{4} + 2\right) = \dfrac{9}{4} \end{align*} $$

Example 2

Let region $R = [0,2]\times[0,1]$ and compute $\displaystyle\iint_R \left(x + 3e^y + \sqrt[3]{y}\right)\,dA$.

Computing an iterated integral one obtains

$$ \begin{align*} \displaystyle\iint_R \left(x + 3e^y + \sqrt[3]{y}\right)\,dA &= \displaystyle\int_0^2\left[\displaystyle\int_0^1 \left(x + 3e^y + \sqrt[3]{y}\right)\,dy\right]dx \\ \\ &= \displaystyle\int_0^2\left[xy + 3e^y + \dfrac{3}{4}y^{4/3}\right]_0^1\,dx \\ \\ &= \displaystyle\int_0^2\left[x + 3e + \dfrac{3}{4} - \left(0 + 3 + 0\right)\right] \,dx \\ \\ &= \displaystyle\int_0^2\left(x + 3e - \dfrac{9}{4}\right)\,dx \\ \\ &= \left[ \dfrac{x^2}{2} + 3ex - \dfrac{9}{4}x\right]_0^2 \\ \\ &= \dfrac{4}{2} + 6e - \dfrac{9}{2} = 6e - \dfrac{5}{2} \end{align*} $$
Just to check our work the other iterated integral yields

$$ \begin{align*} \displaystyle\iint_R \left(x + 3e^y + \sqrt[3]{y}\right)\,dA &= \displaystyle\int_0^1\left[\displaystyle\int_0^2 \left(x + 3e^y + \sqrt[3]{y}\right)\,dx\right]dy \\ \\ &= \displaystyle\int_0^1\left[ \dfrac{x^2}{2} + 3xe^y + x\sqrt[3]{y}\right]_0^2 dy \\ \\ &= \displaystyle\int_0^1\left[ \dfrac{4}{2} + 6e^y + 2\sqrt[3]{y} - \left( 0 + 0 + 0\right)\right]dy \\ \\ &= \left[ 2y + 6e^y + 2\dfrac{3}{4}y^{4/3}\right]_0^1 \\ \\ &= 2 + 6e + \dfrac{3}{2} - \left(0 + 6 + 0\right) = 6e - \dfrac{5}{2} \end{align*} $$

Example 3

Let region $R = [0,1]\times[0,2]$ and compute $\displaystyle\iint_R xe^{x+4y}\,dA$.

Computing an iterated integral one obtains

$$ \begin{align*} \displaystyle\iint_R xe^{x+4y}\,dA &= \displaystyle\int_0^1\left[\displaystyle\int_0^2 xe^{x+4y}\,dy\right] dx \\ \\ &= \displaystyle\int_0^1\left[\displaystyle\int_0^2 xe^xe^{4y}\,dy\right] dx \\ \\ &= \displaystyle\int_0^1 xe^x \left[\displaystyle\int_0^2 e^{4y}\,dy\right] dx \\ \\ &= \displaystyle\int_0^1 xe^x\,dx \cdot \displaystyle\int_0^2 e^{4y}\,dy \\ \\ &= \left[ xe^x - e^x \right]_0^1\,\cdot\,\left[ \dfrac{1}{4}e^{4y} \right]_0^2 \\ \\ &= \left[ e - e - (0 - 1) \right]\,\cdot\,\dfrac{1}{4}\left[ e^8 - e^0 \right] = \dfrac{e^8-1}{4} \end{align*} $$
Just to check our work the other iterated integral yields

$$ \begin{align*} \displaystyle\iint_R xe^{x+4y}\,dA &= \displaystyle\int_0^2\left[\displaystyle\int_0^1 xe^{x+4y}\,dx\right] dy \\ \\ &= \displaystyle\int_0^2\left[ xe^{x + 4y} - e^{x + 4y} \right]_0^1\,dy \\ \\ &= \displaystyle\int_0^2\left[ e^{1+4y} - e^{1+4y} - \left( 0 - e^{4y} \right)\right]\,dy \\ \\ &= \displaystyle\int_0^2 e^{4y}\,dy = \left[\dfrac{1}{4}e^{4y}\right]_0^2 = \dfrac{e^8 - 1}{4} \end{align*} $$

15.1.5 Exercises

Exercise 1

Consider $R = [0,1]\times[1,2]$ and compute $\displaystyle\iint_R \dfrac{y}{x+y^2}\,dA$.

Check your work

Computing an iterated integral yields $$ \begin{align*} \displaystyle\iint_R \dfrac{y}{x+y^2}\,dA &= \displaystyle\int_0^1\left[\displaystyle\int_1^2 \dfrac{y}{x+y^2}\,dy\right] dx \qquad \left| \begin{array}{lcr} u & = & x + y^2 \\ du & = & 2y\,dy \end{array} \right. \\ \\ &= \displaystyle\int_0^1\left[\displaystyle\int_{x+1}^{x+4} \dfrac{du}{2u} \right] dx = \displaystyle\int_0^1\left[\,\dfrac{\ln(u)}{2}\,\right]_{x+1}^{x+4}\ dx \\ \\ &= \dfrac{1}{2}\displaystyle\int_0^1\left(\,\ln(x+4) - \ln(x+1)\,\right)\,dx \\ \\ &= \dfrac{1}{2}\displaystyle\int_0^1\ln(x+4)\,dx - \dfrac{1}{2}\displaystyle\int_0^1\ln(x+1)\,dx \\ \\ &= \dfrac{1}{2}\displaystyle\int_4^5\ln(u)\,du - \dfrac{1}{2}\displaystyle\int_1^2\ln(v)\,dv \qquad \left| \begin{array}{lcr} u & = & x + 4 \\ v & = & x + 1 \end{array} \right. \\ \\ &= \left[\dfrac{u\ln(u) - u}{2}\right]_4^5 - \left[\dfrac{v\ln(v) - v}{2}\right]_1^2 \\ \\ &= \dfrac{ 5\ln(5) - 5 - \left(4\ln(4) - 4\right)}{2} - \dfrac{ 2\ln(2) - 2 - \left(\ln(1)-1\right)}{2} \\ \\ &= \dfrac{ 5\ln(5) - 1 - 4\ln(4)}{2} - \dfrac{\ln(4) - 1}{2} \\ \\ &= \dfrac{ 5\ln(5) - 5\ln(4) }{2} = \dfrac{5}{2}\ln\left(\dfrac{5}{4}\right) \end{align*} $$

Exercise 2

Consider $R = \left[\frac{\pi}{6},\frac{\pi}{3}\right]\times\left[\frac{\pi}{6},\frac{\pi}{3}\right]$ and compute $\displaystyle\iint_R \left(\sin(x) + \cos(y)\right)\,dA$.

Check your work

Computing an iterated integral yields
$$ \begin{align*} \displaystyle\iint_R \left(\sin(x) + \cos(y)\right)\,dA &= \displaystyle\int_{\frac{\pi}{6}}^{\frac{\pi}{3}} \left[ \displaystyle\int_{\frac{\pi}{6}}^{\frac{\pi}{3}} \left(\sin(x) + \cos(y)\right)\,dy\,\right]\,dx \\ \\ &= \displaystyle\int_{\frac{\pi}{6}}^{\frac{\pi}{3}} \left[ y\sin(x) + \sin(y) \right]_{\frac{\pi}{6}}^{\frac{\pi}{3}}\,dx \\ \\ &= \displaystyle\int_{\frac{\pi}{6}}^{\frac{\pi}{3}} \left[ \dfrac{\pi}{3}\sin(x) + \dfrac{\sqrt{3}}{2} - \left( \dfrac{\pi}{6}\sin(x) + \dfrac{1}{2}\right)\right]\,dx \\ \\ &= \displaystyle\int_{\frac{\pi}{6}}^{\frac{\pi}{3}} \left( \dfrac{\pi}{6}\sin(x) + \dfrac{\sqrt{3}-1}{2}\right)\,dx \\ \\ &= \left[ -\dfrac{\pi}{6}\cos(x) + \dfrac{\sqrt{3}-1}{2}x \right]_{\frac{\pi}{6}}^{\frac{\pi}{3}} \\ \\ &= -\dfrac{\pi}{6}\cdot\dfrac{1}{2} + \dfrac{\sqrt{3}-1}{2}\cdot\dfrac{\pi}{3} - \left( -\dfrac{\pi}{6}\cdot\dfrac{\sqrt{3}}{2} + \dfrac{\sqrt{3}-1}{2}\cdot\dfrac{\pi}{6} \right) \\ \\ &= -\dfrac{\pi}{12} + \dfrac{\left(\sqrt{3}-1\right)\pi}{6} - \left(-\dfrac{\pi}{12}\right) = \dfrac{\left(\sqrt{3}-1\right)\pi}{6} \end{align*} $$

15.1.6 Average Value

Just as in functions of one real variable we can compute the average value of a function defined on a rectangle $R = [a,b]\times[c,d]$. The average value is defined

$$ f_{\text{avg}} := \dfrac{1}{A(R)}\displaystyle\iint_R f(x,y)\,dA $$
where $A(R)$ is the area of the rectangle. Thus

$$ A(R)\,\cdot\,f_{\text{avg}} = \displaystyle\iint_R f(x,y)\,dA $$
This means that the box with base $R$ and height $f_{\text{avg}}$ has the same volume as the solid under the surface $z = f(x,y)$ over $R$.

For a continuous surface we have the mean value theorem for double integrals over a rectangle .

Theorem 15.1.2

Mean Value Theorem for Double Integrals Over a Rectangle
If $f:R\rightarrow\mathbb{R}$ is a continuous function defined on a rectangle $R = [a,b]\times[c,d]$, then there is a point in the rectangle $\left(\overline{x},\overline{y}\right)\in R$ such that

$$ f_{\text{avg}} = f\left(\overline{x},\overline{y}\right) = \dfrac{1}{A(R)}\displaystyle\iint_R f(x,y)\,dA $$

The proof of this theorem is an exercise in the review test for Chapter 15.

15.1.7 Exercises

Exercise 3

Consider $R = [0,1]\times[1,2]$ and compute the average value of the function $f(x,y) = xe^{x-y}$ over this rectangle.

Check your work

Computing an iterated integral yields
$$ \begin{align*} f_{\text{avg}} &= \frac{1}{A(R)}\displaystyle\int_0^1\left[\displaystyle\int_1^2 xe^{x-y}\,dy\right]\,dx \\ \\ &= \dfrac{1}{(1-0)(2-1)}\displaystyle\int_0^1\left[\displaystyle\int_1^2 xe^xe^{-y}\,dy\right]\,dx \\ \\ &= \displaystyle\int_0^1xe^x\,dx\,\cdot\,\displaystyle\int_1^2 e^{-y}\,dy \\ \\ &= \left[ xe^x - e^x \right]_0^1\,\cdot\,\left[ -e^{-y} \right]_1^2 \\ \\ &= \left[ e - e - (0 - 1) \right]\,\cdot\,\left[ -e^{-2} - (-e^{-1}) \right] \\ \\ &= \dfrac{1}{e} - \dfrac{1}{e^2} \end{align*} $$

Your use of this self-initiated mediated course material is subject to our Creative Commons License .

Creative Commons Attribution-NonCommercial-ShareAlike 4.0


Attribution
You must give appropriate credit, provide a link to the license, and indicate if changes were made. You may do so in any reasonable manner, but not in any way that suggests the licensor endorses you or your use.


Noncommercial
You may not use the material for commercial purposes.


Share Alike
You are free to share, copy and redistribute the material in any medium or format. If you adapt, remix, transform, or build upon the material, you must distribute your contributions under the same license as the original.