Math 344: Calculus III

16.2 Path Integrals

---

16.2.1 Arc Length

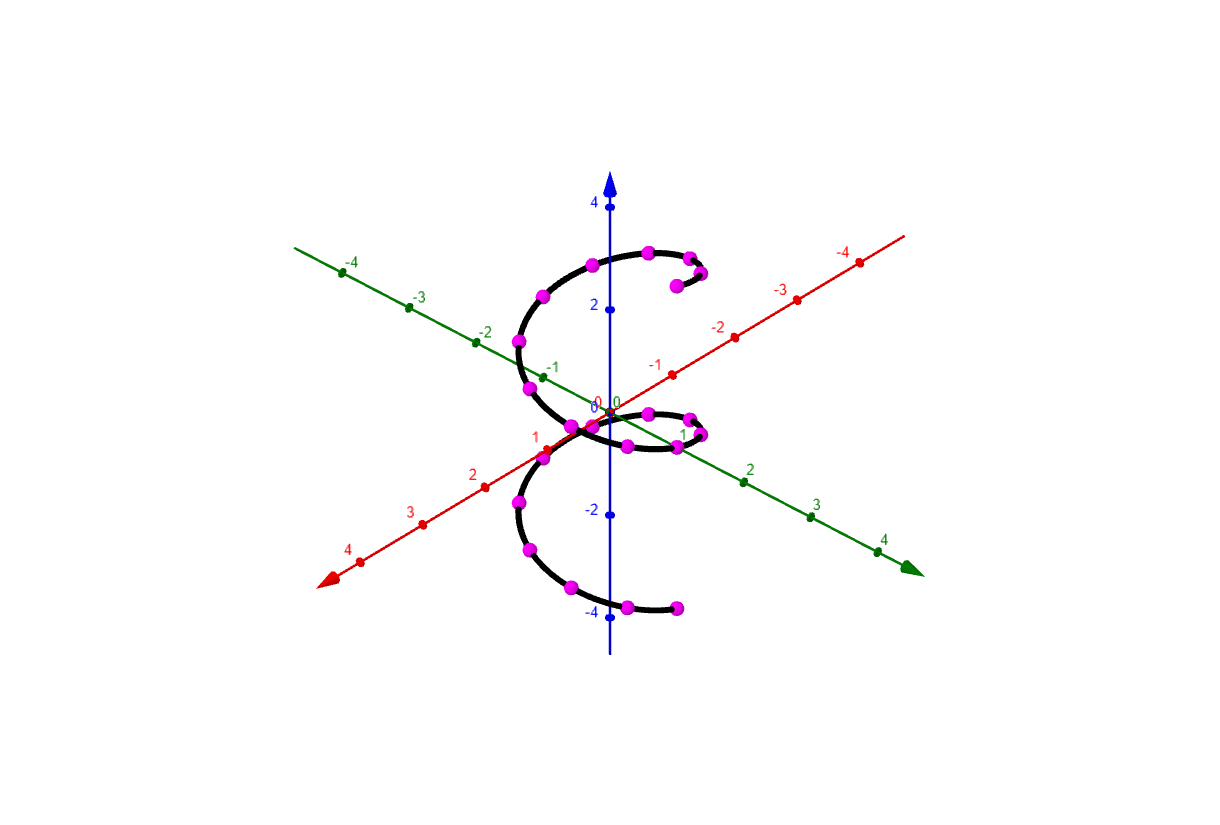
In Chapter 13 we discussed arc length of a trajectory or path in $\mathbb{R}^n \require{color} \definecolor{brightblue}{rgb}{.267, .298, .812} \definecolor{darkblue}{rgb}{.08, .18, .28} \definecolor{palepink}{rgb}{1, .73, .8} \definecolor{softmagenta}{rgb}{.99,.34,.86} \def\ihat{\mathbf{\hat{\mmlToken{mi}[mathvariant="bold"]{ı}}}} \def\jhat{\mathbf{\hat{\mmlToken{mi}[mathvariant="bold"]{ȷ}}}} \def\khat{\mathbf{\hat{k}}} \newcommand{\pypx}[2][x]{\dfrac{\partial #2}{\partial #1}} \newcommand{\dydx}[2][x]{\dfrac{d #2}{d #1}} \newcommand{\deltax}[2][x]{\frac{\Delta #2}{\Delta #1}} \newcommand{\rb}[1][r]{\mathbf{#1}} \newcommand{\rt}[1][t]{\rb(#1)}$.

$\rt$	Segmented Helix

Figure 1

Given a parameterization of the path in $\mathbb{R}^n$, say

$$ \rt = \left( \sin(2t), \cos(2t), t \right),\qquad t\in\left[-\pi, \pi\right] $$
one divides the domain of the path into a finite number of segments

$$ -\pi = t_0 < t_1 < t_2 < t_3 < \dots < t_{n-1} < t_n = \pi $$
and approximates the length of each segment of the path by the length of the velocity vector at the left end point of each segment of the domain.

$$ \rb(-\pi) = P_0 < P_1 < P_2 < P_3 < \dots < P_{n-1} < P_n = \rb(\pi) $$

$\mathbf{\rb}(t)$	Segmented Helix

Figure 2

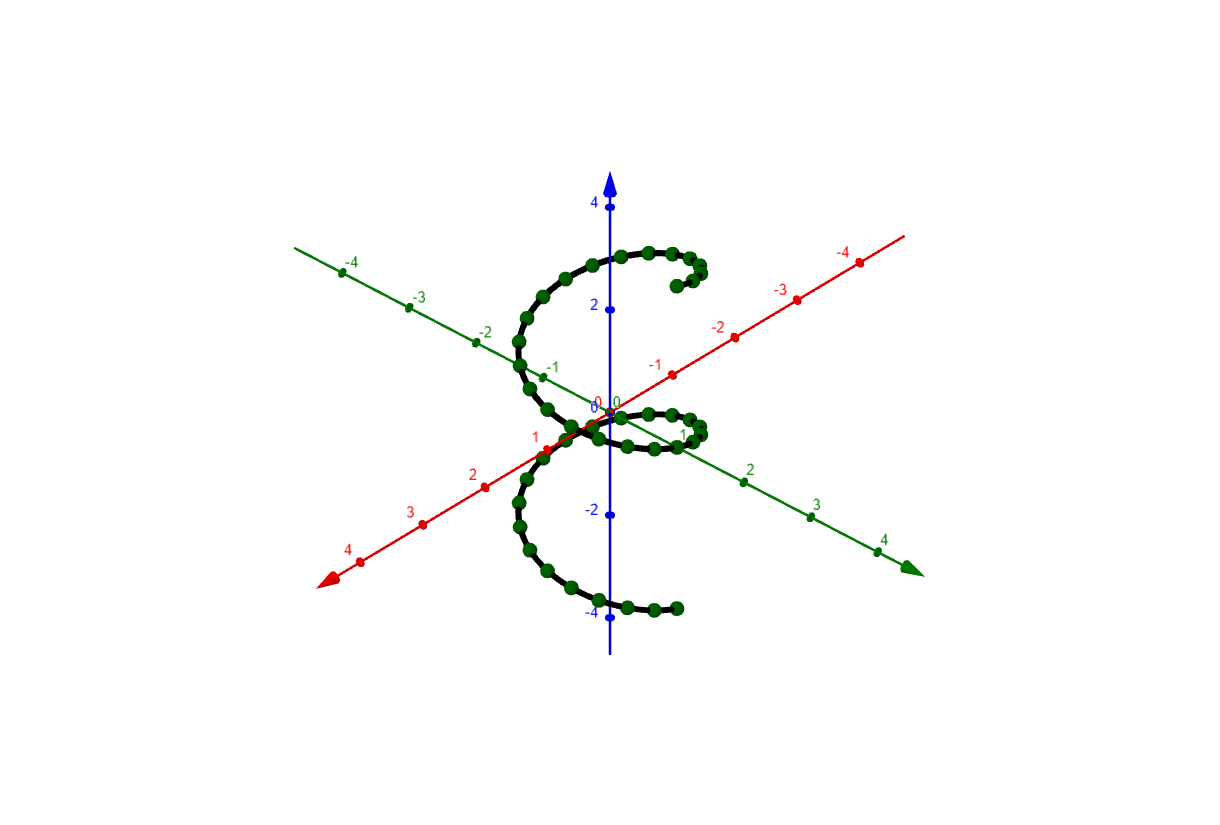
We approximate the length of each arc segment with the length of the velocity vector scaled by the length of the segment in the domain,

$$ \left\|\rb\,'(t)\right\|\Delta t $$

$\rb\,'(t)$	Arc Length Approximation

Figure 3

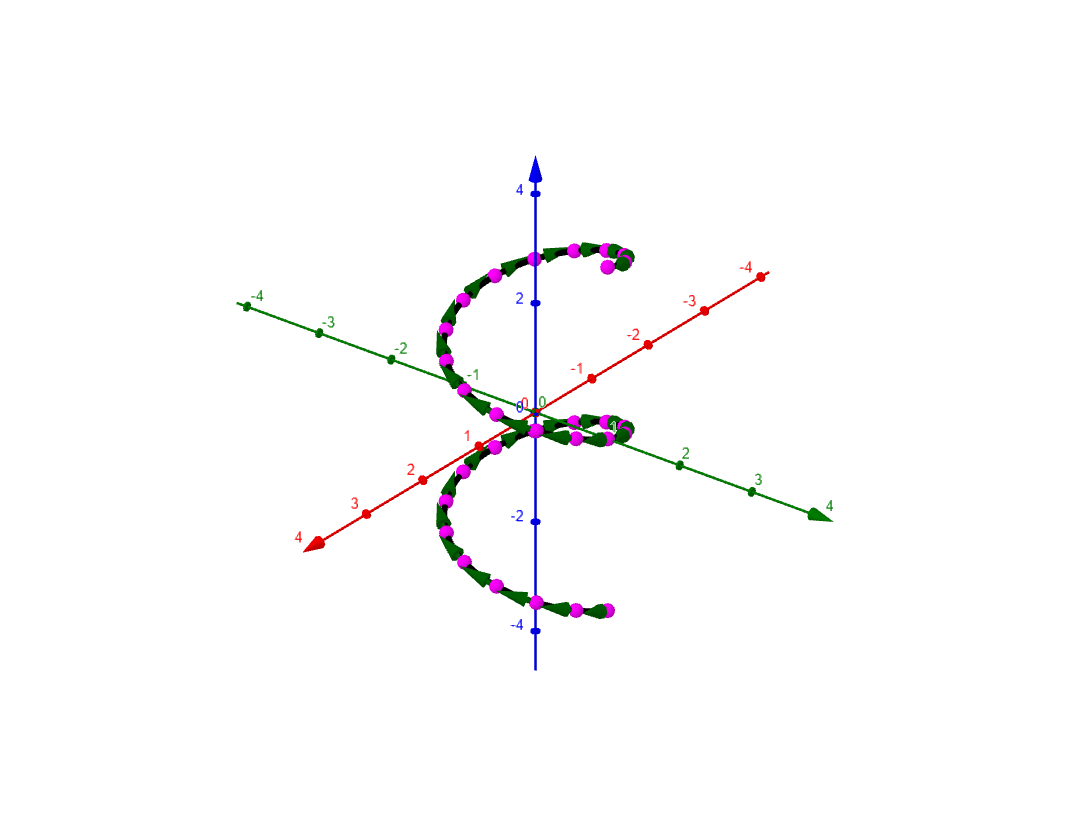
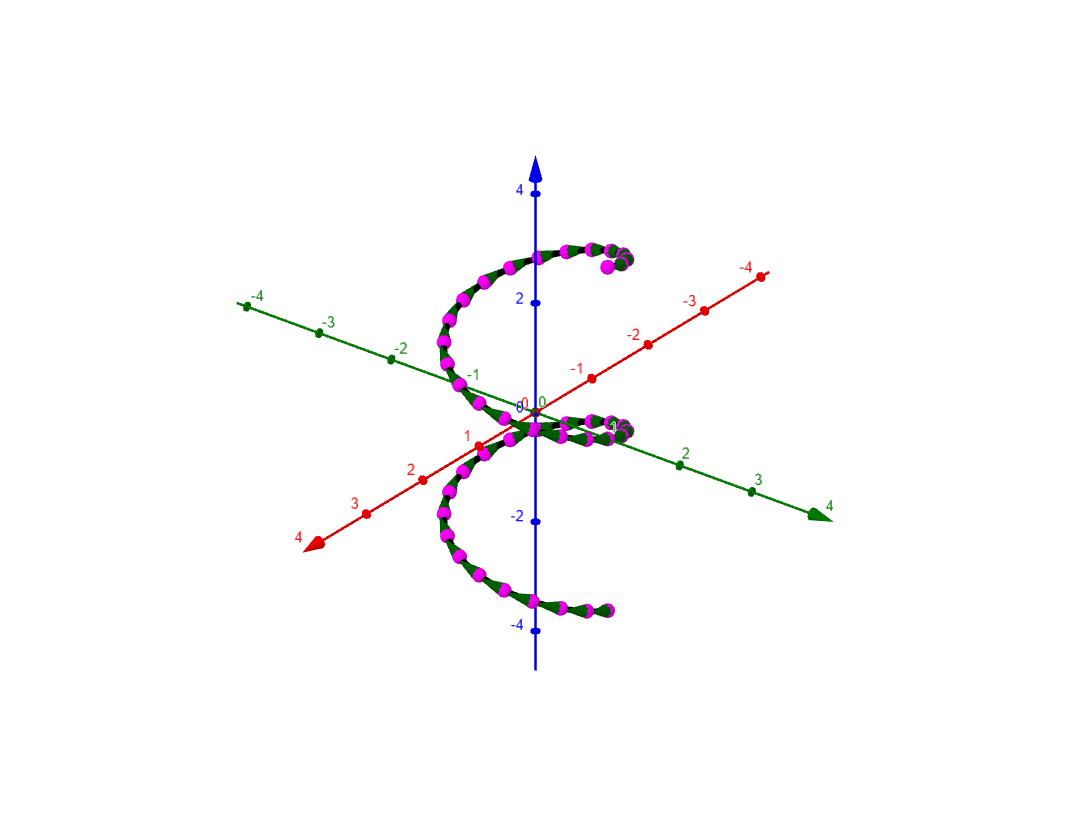
Adding these approximations of length one obtains a Riemann sum

$$ \text{Arc Length} \approx\,\displaystyle\sum_{k=1}^n \left\|\rb\,'(t)\right\|\Delta t $$
Computing the limit as $n\rightarrow\infty$ results in the arc length defined as a definite integral

$$ \text{Arc Length} = s = \displaystyle\lim_{n\rightarrow\infty}\,\displaystyle\sum_{k=1}^n \left\|\rb'(t)\right\|\Delta t = \displaystyle\int_{-\pi}^{\pi} \left\|\rb\,'(t)\right\|\,dt $$
This yields a definition for arc length for a path parameterized by vector function $\rb:[a,b]\rightarrow\mathbb{R}^n$ by

$$ \text{Arc Length} = s = \displaystyle\int_a^b \left\|\rb\,'(t)\right\|\,dt $$
If $t\in[a,b]$, then we can define the arc length function $s:[a,b]\rightarrow\mathbb{R}$, by

$$ s(t) := \displaystyle\int_a^t \left\|\rb\,'(\tau)\right\|\,d\tau $$
Using Leibniz Rule rule one can compute the derivative

$$ \dfrac{ds}{dt} = \left\|\rb\,'(t)\right\| $$

16.2.2 Arc Length in $\mathbb{R}^2$

In $\mathbb{R}^2$, our vector function $\rb:[a,b]\rightarrow\mathbb{R}^2$ outputs a vector with two coordinates $\rb(t) = \begin{bmatrix} x \\ y \end{bmatrix}$ for every $t\in[a,b]$. This gives us two coordinate functions $x:[a,b]\rightarrow\mathbb{R}$ and $y:[a,b]\rightarrow\mathbb{R}$ so that

$$ \rb(t) = \langle x(t), y(t) \rangle $$
Thus

$$ \rb\,'(t) = \langle x'(t), y'(t) \rangle $$
and
$$ \left\|\rb'(t)\right\| = \sqrt{\left(\dfrac{dx}{dt}\right)^2 + \left(\dfrac{dy}{dt}\right)^2} $$
Hence arc length is given by

$$ s = \displaystyle\int_a^b \left\|\rb\,'(t)\right\|\,dt = \displaystyle\int_a^b \sqrt{\left(\dfrac{dx}{dt}\right)^2 + \left(\dfrac{dy}{dt}\right)^2}\,dt $$
Likewise the arc length function becomes

$$ s(t) = \displaystyle\int_a^t \left\|\rb'(\tau)\right\|\,d\tau = \displaystyle\int_a^t \sqrt{\left(\dfrac{dx}{d\tau}\right)^2 + \left(\dfrac{dy}{d\tau}\right)^2}\,d\tau $$
When $t=b$ we refer to the integral as a path integral over the curve , where the curve $C = \rb\left([a,b]\right)$ is the image of $\rb$ in $\mathbb{R}$, and write this path integral

$$ \text{Arc Length} = s = \displaystyle\int_C\,ds $$
This notation emphasizes that we integrate over the curve $C$ instead of over an interval of the real line. This notation is justified by our observation that

$$ \dfrac{ds}{dt} = \left\|\rb\,'(t)\right\| $$
and so in differential form we have

$$ ds = \left\|\rb'(t)\right\|dt $$
Using the Chain Rule yields

$$ \text{Arc Length} = s = \displaystyle\int_C\,ds = \displaystyle\int_{\rb(a)}^{\rb(b)}\,ds = \displaystyle\int_a^b \left\|\rb'(t)\right\|\,dt $$

16.2.3 Path Integral with Respect to Arc Length

Just as arc length is computed in $\mathbb{R}^2$, one may compute arc length in $\mathbb{R}^n$ using the same formula

$$ \text{Arc Length} = s = \displaystyle\int_C\,ds = \displaystyle\int_{\rb(a)}^{\rb(b)}\,ds = \displaystyle\int_a^b \left\|\rb'(t)\right\|\,dt $$

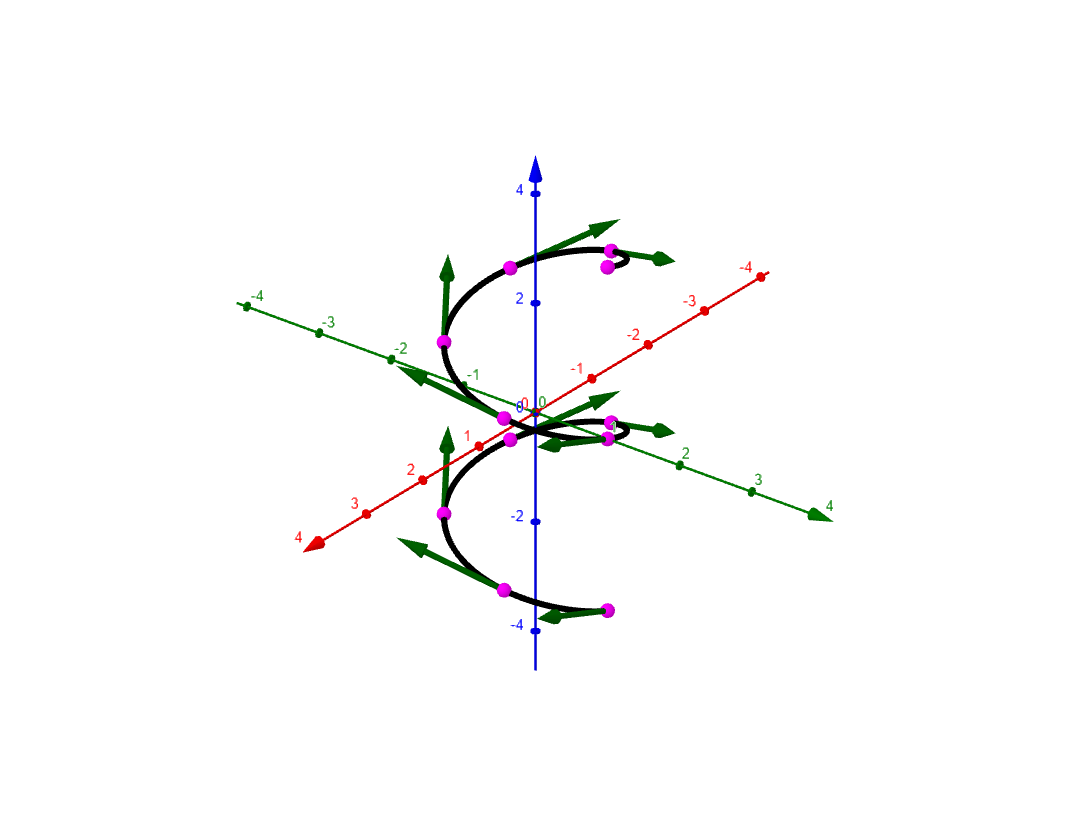
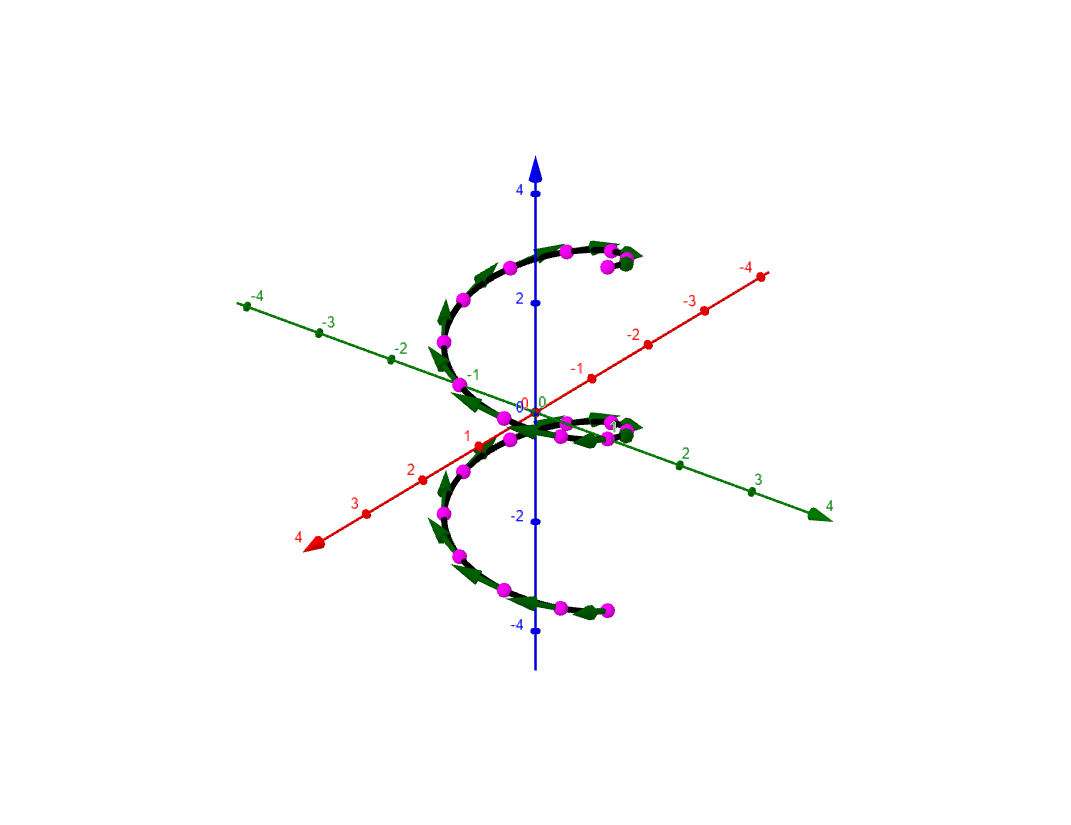
In the computation of arc length the integrand is always a $1$. However we can also compute a Riemann sum using a function of our independent variables along the curve $C$ by

$$ \displaystyle\sum_{k=1}^n f(x_k^*,y_k^*)\,\Delta s_k $$
where $(x_k^*,y_k^*)$ is a point on arc $s_k$, and curve $C$ is partitioned into smaller arcs $\left\{ s_1, s_2, \dots, s_n \right\}$ as in figure 1. If the limit exists we define the path integral or path integral with respect to arc length . For example in $\mathbb{R}^3$ we have a continuous function $f:\mathbb{R}^n\rightarrow\mathbb{R}$, and a curve $C$ in $\mathbb{R}^3$. The path integral of $f$ on $C$ is defined by

$$ \displaystyle\int_C f(x,y,z)\,ds := \displaystyle\lim_{n\rightarrow\infty}\displaystyle\sum_{k=1}^n f(x_k^*)\,\Delta s_k $$

Figure 4

This path integral can be computed just as for arc length


$$ \displaystyle\int_C f(x,y,z)\,ds = \displaystyle\int_{\rb(a)}^{\rb(b)} f(x,y,z)\,ds = \displaystyle\int_a^b f(x,y,z)\,\left\|\rb'(t)\right\|\,dt $$

where $\rb(t)$ is a parameterization of curve $C$.

Definition

If the graph of $f:\mathbb{R}\rightarrow\mathbb{R}^n$ is a function and curve $C$ is a piecewise continuous curve in $\mathbb{R}^n$, then the path integral of $f$ with respect to arc length over $C$ is given by

$$ \displaystyle\int_C f(x_1,x_2,\dots,x_n)\,ds = \displaystyle\int_{\rb(a)}^{\rb(b)} f(x_1,x_2,\dots,x_n)\,ds = \displaystyle\int_a^b f(x_1(t),x_2(t),\dots,x_n(t))\,\left\|\rb'(t)\right\|\,dt $$

16.2.4 Examples

Example 16.2.1

Consider the curve $C$, where $C$ is the right half of the circle of radius 2 centered at the origin. What is the length of the curve?

Consider the graph of the curve $x^2 + y^2 = 4$, $x\ge 0$.

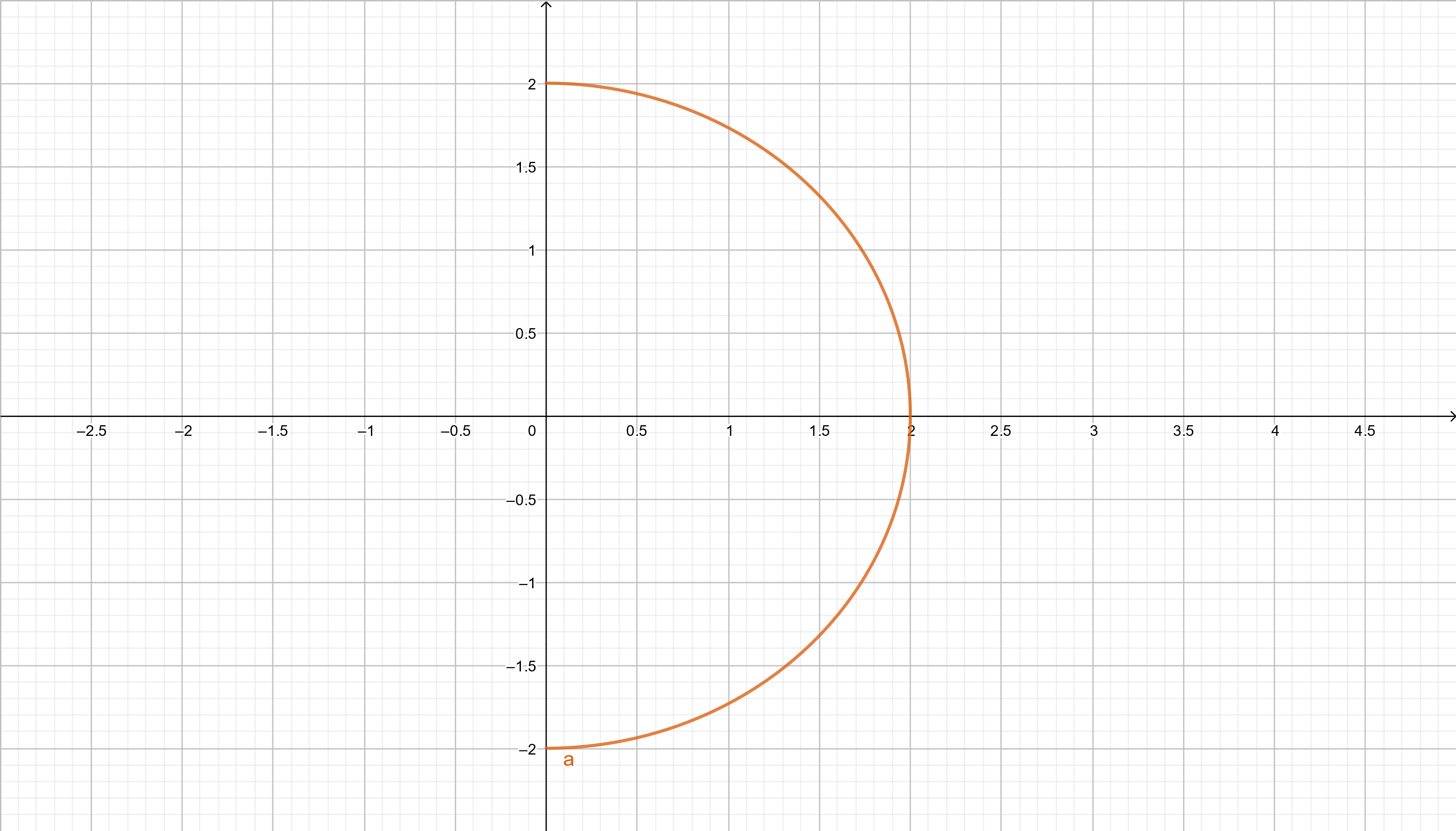Figure 5

$$ \rt = \langle 2\cos(t),\ 2\sin(t)\rangle,\qquad t\in\left[ -\dfrac{\pi}{2}, \dfrac{\pi}{2} \right] $$
The length of this path is given by

$$ \begin{align*} \text{length } &= \displaystyle\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\left\|\rb\,'(t)\right\|\,dt \\ &= \displaystyle\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\sqrt{\left(\dfrac{dx}{dt}\right)^2 + \left(\dfrac{dy}{dt}\right)^2}\,dt \\ \\ &= \displaystyle\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\sqrt{\left(-2\sin(t)\right)^2 + \left(2\cos(t)\right)^2}\,dt \\ \\ &= \displaystyle\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\sqrt{4\sin^2(t) + 4\cos^2(t)}\,dt \\ \\ &= \displaystyle\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\sqrt{4}\,dt = 2\,\displaystyle\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\,dt = 2\left[ t \right]_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \\ &= 2\left(\frac{\pi}{2} - \left(-\frac{\pi}{2}\right)\right) = 2\pi \end{align*} $$
We can check this using the formula for the diameter of a circle of radius two. The diameter is $2\pi r$, so our semi-circular path has length $r\pi = 2\pi$.

Example 16.2.2

Evaluate $\displaystyle\int_C x^2\,ds$, where $C$ is the curve $y=x+1$ from $(0,0)$ to $(1,2)$.

figure 6

One must parameterize the path from $(0,0)$ to $(1,2)$. One parameterization of a line segment from vector $\overline{x}_0$ to $\overline{x}_1$ is given by

$$ \rb(t) = \overline{x}_0\,(1-t) + \overline{x}_1\,t,\qquad t\in[0,1] $$
In this exercise our parameterization becomes

$$ \rb(t) = \langle 0,0\rangle\,(1-t) + \langle 1,2\rangle\,t = \langle t, 2t \rangle = \langle x(t), y(t) \rangle,\qquad t\in[0,1] $$
Hence our integral may be evaluated

$$ \begin{align*} \displaystyle\int_C x^2\,ds &= \displaystyle\int_C x^2(t)\,\left\|\rb'(t)\right\|\,dt \\ \\ &= \displaystyle\int_0^1 t^2\,\left\|\langle 1,2 \rangle\right\|\,dt \\ \\ &= \displaystyle\int_0^1 t^2 \,\sqrt{1^2 + 2^2}\,dt \\ \\ &= \sqrt{5}\left[ \dfrac{t^3}{3} \right]_0^1 = \dfrac{\sqrt{5}}{3} \end{align*} $$

Example 16.2.3

A spring takes the shape of a helix

$$ \overline{r}(t) = \left\langle \cos(t), \sin(t), \frac{t}{6\pi} \right\rangle,\qquad t\in[0,6\pi] $$

figure 7

The spring is not one dimensional. Instead the curve $C(t) = \left\langle \cos(t), \sin(t), \frac{t}{6\pi} \right\rangle$ describes the center of a wire that makes up the spring of uniform width so that the cross-sectional area of the wire is $A = \pi r^2 = $ constant. The wire is more dense at the base of the spring than the top. The density diminishes linearly from the base to the top according to the function

$$ \rho(x,y,z) = 2 - z $$
so that at the base the wire has a density of $\rho(0) = A(2 - 0) = 2A\frac{\text{g}}{\text{cm}^3}$, and at the top has a density of $\rho(1) = A(2 - 1) = A\frac{\text{g}}{\text{cm}^3}$. Find the center of gravity of the spring.

First one computes the mass of the spring. To simplify our computations we consider the wire to be one dimensional path of the center of the wire $C$.

$$ \begin{align*} m = \displaystyle\int_{C} \rho(x,y,z)\,ds &= \displaystyle\int_0^{6\pi} A\,(2-z)\,\left\|\rb'(t)\right\|\,dt \\ \\ &= A\,\displaystyle\int_0^{6\pi} \left(2 - \frac{t}{6\pi}\right)\,\left\|\left\langle -\sin(t),\cos(t),\frac{1}{6\pi}\right\rangle\right\|\,dt \\ \\ &= A\,\displaystyle\int_0^{6\pi} \left(2 - \frac{t}{6\pi}\right)\,\sqrt{\sin^2(t) + \cos^2(t) + \frac{1}{36\pi^2}}\,dt \\ \\ &= A\,\sqrt{\frac{1+36\pi^2}{36\pi^2}}\,\displaystyle\int_0^{6\pi} \left(2 - \frac{t}{6\pi}\right)\,dt \\ \\ &= A\,\frac{\sqrt{1+36\pi^2}}{6\pi}\,\left[ 2t - \frac{t^2}{12\pi} \right]_0^{6\pi} \\ \\ &= A\,\frac{\sqrt{1+36\pi^2}}{6\pi}\,\left[ 12\pi - \frac{36\pi^2}{12\pi} \right] \\ \\ &= A\,\sqrt{1 + 36\pi^2}\,\left[ 2 - \frac{6\pi}{12\pi}\right] = \frac{3A\sqrt{1 + 36\pi^2}}{2} \end{align*} $$
Now we need $\overline{x}$

$$ \begin{align*} \overline{x} &= \frac{\displaystyle\int_C x\rho(x,y,z)\,ds}{m} = \frac{A}{m}\,\displaystyle\int_0^{6\pi} x(2-z)\left\| \rb'(t) \right\|\,dt \\ \\ &= \frac{2}{3\sqrt{1 + 36\pi^2}}\,\displaystyle\int_0^{6\pi} \cos(t)\left(2 - \frac{t}{6\pi}\right)\,\sqrt{\sin^2(t) + \cos^2(t) + \frac{1}{36\pi^2}}\,dt \\ \\ &= \frac{2}{18\pi}\,\displaystyle\int_0^{6\pi} \cos(t)\left(2 - \frac{t}{6\pi}\right)\,dt \qquad {\color{blue} \begin{vmatrix} 2 - \frac{t}{6\pi} & \qquad & \cos(t)\,dt \\ -\frac{1}{6\pi} & \qquad & \sin(t) \\ 0 & \qquad & -\cos(t) \end{vmatrix} } \\ \\ &= \frac{1}{9\pi}\,\left[ \left(2 - \frac{t}{6\pi}\right)\sin(t) - \frac{1}{6\pi}\cos(t) \right]_0^{6\pi} = 0 \\ \end{align*} $$
Similarly, $\overline{y} = 0$.

$$ \begin{align*} \overline{z} &= \frac{\displaystyle\int_C z\rho(x,y,z)\,ds}{m} = \frac{A}{m}\,\displaystyle\int_0^{6\pi} z(2-z)\left\| \rb'(t) \right\|\,dt \\ \\ &= \frac{2}{3\sqrt{1 + 36\pi^2}}\,\displaystyle\int_0^{6\pi} \frac{t}{6\pi}\,\left(2 - \frac{t}{6\pi}\right)\,\sqrt{\sin^2(t) + \cos^2(t) + \frac{1}{36\pi^2}}\,dt \\ \\ &= \frac{2}{108\pi^2}\,\displaystyle\int_0^{6\pi} t\,\left(2 - \frac{t}{6\pi}\right)\,dt \\ \\ &= \frac{1}{54\pi^2}\,\displaystyle\int_0^{6\pi} \left(2t - \frac{t^2}{6\pi}\right)\,dt \\ \\ &= \frac{1}{54\pi^2}\,\left[ t^2 - \frac{t^3}{18\pi}\right]_0^{6\pi} = \frac{1}{54\pi^2}\,\left[ 36\pi^2 - \frac{216\pi^3}{18\pi} \right] \\ \\ &= \frac{1}{54\pi^2}\,\left[ 36\pi^2 - 12\pi^2 \right] = \frac{1}{54\pi^2}\cdot 24\pi^2 = \frac{4}{9} \end{align*} $$
The center of mass is located at $\left\langle 0, 0, \frac{4}{9}\right\rangle$.

16.2.5 Exercises

Exercise 16.2.1

Evaluate the path integral $\displaystyle\int_C x^2y\,ds$, where curve $C$ is the helix defined by

$$ \rb(t) = \left\langle \cos(t), \sin(t), t \right\rangle,\qquad 0\le t\le \frac{\pi}{2} $$

Check your work

Computing the path integral yields
$$ \begin{align*} \displaystyle\int_C x^2y\,ds &= \displaystyle\int_0^{\pi/2} x^2y\,\left\|\rb'(t)\right\|\,dt \\ \\ &= \displaystyle\int_0^{\pi/2} \cos^2(t)\,\sin(t)\,\sqrt{(-\sin)^2(t) + \cos^2(t)+1^2}\,dt \\ \\ &= \displaystyle\int_0^{\pi/2} \cos^2(t)\,\sin(t)\,\sqrt{2}\,dt \qquad {\color{blue} \left|\begin{array}{c} u = \cos(t) \\ du = -\sin(t)\,dt \\ \\ u(0) = 1 \\ u(\pi/2) = 0 \end{array}\right.} \\ \\ &= \sqrt{2}\,\displaystyle\int_1^0 u^2\,(-du) = \sqrt{2}\,\displaystyle\int_0^1 u^2\,(du) \\ \\ &= \sqrt{2}\left[\,\dfrac{u^3}{3}\,\right]_0^1 = \dfrac{\sqrt{2}}{3} \end{align*} $$

Exercise 16.2.2

Evaluate the path integral $\displaystyle\int_C x^2 + y^2 + z^2\,ds$, where curve $C$ is the circle in $\mathbb{R}^3$ defined by

$$ \rb(t) = \left\langle 1, \cos(2t), \sin(2t) \right\rangle,\qquad 0\le t\le 2\pi $$

Check your work

Computing the path integral yields
$$ \begin{align*} \displaystyle\int_C x^2 + y^2 + z^2\,ds &= \displaystyle\int_0^{2\pi} \left(\,x^2 + y^2 + z^2\,\right)\,\left\|\rb'(t)\right\|\,dt \\ \\ &= \displaystyle\int_0^{2\pi} \left(\,1^2 + \cos^2(2t) + \sin^2(2t)\,\right)\,\sqrt{1^2 + \left(-\sin(2t)\right)^2 + \cos^2(2t)}\,dt \\ \\ &= 2\sqrt{2}\,\displaystyle\int_0^{2\pi}\,dt = 4\pi\sqrt{2} \end{align*} $$

16.2.6 Path Integrals in Vector Fields

In Section 12.3 we computed the work done by a constant force $\rb[F]$ moving an object from point $P$ to point $Q$ in space is given by $W = \rb[F]\cdot\rb[D]$, where $\rb[D]=\overrightarrow{PQ}$.

$$ \text{Work} = \text{force in the direction of }\rb[D]\times\text{distance} = \text{Comp}_{\rb[D]}\rb[F]\,\cdot\,\|\rb[D]\| = \rb[F]\cdot\rb[D] $$
Just as above, this formula works equally well in $\mathbb{R}^n$. If $\rb[F],\rb[D]\in\mathbb{R}^n$, then the work done by a force $\rb[F]$ acting moving a particle from the base of $\rb[D]$ to its tip is

$$ W = \rb[F]\cdot\rb[D] $$

If the particle follows a path $C$ in $\mathbb{R}^3$ that starts at point $\rb(a)$ and ends at point $\rb(b)$, then we can divide the curve into arcs at points $\rb(a) = P_0, P_1, P_2, \dots, P_n = \rb(b)$. On each arc from $P_{k-1}$ to $P_k$ we choose a point

$$ P_k^* = P(t_k^*) = P(x(t_k^*),y(t_k^*),z(t_k^*)),\qquad t_k^*\in[t_{k-1},t_k] $$
and approximate the length of the by the tangent vector to the curve scaled by the arc length $\Delta s_k$ of each arc.

$$ \rb[T](t_k^*)\,\Delta s_k $$
Further we approximate the work done by the force acting on the particle on the arc by

$$ W_k = \rb[F]\cdot\rb[T](t_k^*)\,\Delta s_k $$

We add these approximations for each arc to get an approximation to the total work

$$ W \approx \displaystyle\sum_{k=1}^n W_k = \displaystyle\sum_{k=1}^n \rb[F]\cdot\rb[T](t_k^*)\,\Delta s_k $$
We compute the limit of this Riemann sum to obtain

$$ W = \displaystyle\lim_{n\rightarrow\infty}\displaystyle\sum_{k=1}^n W_k = \displaystyle\lim_{n\rightarrow\infty}\displaystyle\sum_{k=1}^n \rb[F]\cdot\rb[T](t_k^*)\,\Delta s_k = \displaystyle\int_C \rb[F]\cdot\rb[T]\,ds = $$
We simplify this expression to obtain

$$ W = \displaystyle\int_C \rb[F]\cdot\rb[T]\,ds = \displaystyle\int_a^b \rb[F]\left(\rb(t)\right)\cdot\dfrac{\rb'(t)}{\left\|\rb'(t)\right\|}\,\left\|\rb'(t)\right\|\,dt = \displaystyle\int_a^b \rb[F]\left(\rb(t)\right)\cdot\rb'(t)\,dt $$
By definition

$$ \dfrac{d\rb}{dt} = \rb'(t) $$
so we may write

$$ d\rb = \rb'(t)\,dt $$
Thus

$$ W = \displaystyle\int_C \rb[F]\cdot\rb[T]\,ds = \displaystyle\int_a^b \rb[F]\cdot\rb'(t)\,dt = \displaystyle\int_C \rb[F]\cdot d\rb $$

16.2.7 Examples

Example 16.2.4

We can picture the force due to gravity at each point on a curve in space pointing directly toward the origin or center of gravity for our vector field.

figure 8

However a particle is moving along path $C$ with tangent vectors at each point.

figure 9

When the force due to gravity points somewhat the same direction as the motion of the particle on the curve, gravity will accelerate the particle along the curve and the projection vector of gravity $\rb[F]$ will point along the tangent vector $\rb[T]$. However if path along the curve moves away from the origin, gravity will decelerate the particle along the curve and the projection vector of gravity will point in the opposite direction to the tangent vector. If we zoom into the curve we will see several projection vectors. Since the length of the tangent vector is 1, we have that

$$ \text{Proj}_{\rb[T]}\rb[F] = \left(\rb[F]\cdot\rb[T]\right)\,\rb[T] $$

figure 10

Example 16.2.5

Evaluate $\displaystyle\int_C \rb[F]\cdot d\rb$, where $\rb[F] = (xy)\ihat + y^2\jhat$, and $C$ is the circle with radius 2 and center at the origin. The particle is traveling counter-clockwise on the circle from $(2,0)$ to $(2,0)$.

We need an appropriate parameterization of the circle.

$$ \rb(t) = \langle<2\cos(t), 2\sin(t)\rangle,\qquad t\in[0,2\pi] $$

$$ \begin{align*} \displaystyle\int_C \rb[F]\cdot d\rb &= \displaystyle\int_0^{2\pi} \left\langle xy, y^2 \right\rangle\cdot\left\langle -2\sin(t), 2\cos(t)\right\rangle\,dt \\ \\ &= \displaystyle\int_0^{2\pi} \left\langle 4\sin(t)\cos(t), 4\sin^2(t) \right\rangle\cdot\left\langle -2\sin(t), 2\cos(t)\right\rangle\,dt \\ \\ &= \displaystyle\int_0^{2\pi} -8\sin^2(t)\cos(t) + 8\sin^2(t)\cos(t)\,dt = 0 \\ \end{align*} $$

Example 16.2.6

Evaluate $\displaystyle\int_C \rb[F]\cdot d\rb$, where $\rb[F] = \langle y+z, 2xz, x+z\rangle$ and $C$ is the curve defined by

$$ \begin{align*} x &= 2t+1 \\ y &= 3t-1 \\ z &= -t+2, \end{align*} $$ where $0\le t\le2$.

The definition of curve $C$ is a line segment in parametric form so our vector-valued function for our line segment is $\rb(t) = \langle 2t+1, 3t-1, -t+2\rangle$, where $t\in[0,2]$. Hence

$$ \begin{align*} \displaystyle\int_C \rb[F]\cdot d\rb &= \displaystyle\int_0^2 \left\langle y+z, 2xz, x+z \right\rangle\cdot\left\langle 2,3,-1 \right\rangle\,dt \\ \\ &= \displaystyle\int_0^2 \left\langle (3t-1)+(-t+2), 2(2t+1)(-t+2), (2t+1)+(-t+2) \right\rangle\cdot\left\langle 2,3,-1 \right\rangle\,dt \\ \\ &= \displaystyle\int_0^2 \left\langle 2t+1, 2(-2t^2+3t+2), t+3\right\rangle\cdot\left\langle 2,3,-1 \right\rangle\,dt \\ \\ &= \displaystyle\int_0^2 2(2t+1) + 6(-2t^2+3t+2) - (t+3)\,dt \\ \\ &= \displaystyle\int_0^2 11 + 21t - 12t^2\,dt = \left[ 11t + \frac{21t^2}{2} - 4t^3 \right]_0^2 \\ \\ &= 22 + 42 - 32 = 32 \end{align*} $$

16.2.8 Path Integrals in $\mathbb{R}^3$

Suppose that our vector field is given by

$$ \rb[F](x,y,z) = \left\langle P(x,y,z), Q(x,y,z), R(x,y,z) \right\rangle $$
as a vector-valued function of each point in $\mathbb{R}^3$ with coordinate functions $P(x,y,z)$, $Q(x,y,z)$, and $R(x,y,z)$. Given a parameterization of curve $C$ given by $\rb(t) = \langle x(t), y(t), z(t)\rangle$ for $t\in[a,b]$, we compute the path integral of curve $C$ in vector field $\rb[F]$ as

$$ \begin{align*} \displaystyle\int_C \rb[F]\cdot\,d\rb &= \displaystyle\int_a^b \left\langle P, Q, R \right\rangle\cdot\,\rb'(t)\,dt \\ \\ &= \displaystyle\int_a^b \left\langle P(x(t),y(t),z(t)), Q(x(t),y(t),z(t)), R(x(t),y(t),z(t)) \right\rangle\cdot\,\left\langle x'(t),y'(t),z'(t) \right\rangle\,dt \\ \\ &= \displaystyle\int_a^b P(x(t),y(t),z(t))\,x'(t) + Q(x(t),y(t),z(t))\,y'(t) + R(x(t),y(t),z(t))\,z'(t)\,dt \\ \\ &= \displaystyle\int_a^b P(x(t),y(t),z(t))\,x'(t)\,dt + \displaystyle\int_a^b Q(x(t),y(t),z(t))\,y'(t)\,dt \\ &\qquad\qquad + \displaystyle\int_a^b R(x(t),y(t),z(t))\,z'(t)\,dt \\ \end{align*} $$
Using

$$ dx = x'(t)\,dt\qquad dy = y'(t)\,dt\qquad dz = z'(t)\,dt $$
we write

$$ \begin{align*} \displaystyle\int_C \rb[F]\cdot\,d\rb &= \displaystyle\int_C P(x,y,z)\,dx + \displaystyle\int_C Q(x,y,z)\,dy + \displaystyle\int_C R(x,y,z)\,dz \\ \\ &= \displaystyle\int_C P(x,y,z)\,dx + Q(x,y,z)\,dy + R(x,y,z)\,dz \\ \\ &= \displaystyle\int_C Pdx + Qdy + Rdz \end{align*} $$
In $\mathbb{R}^2$ we have

$$ \displaystyle\int_C \rb[F]\cdot\,d\rb = \displaystyle\int_C Pdx + Qdy $$

Example 16.2.7

A force $\rb[F] = (3x-4y)\,\ihat + (4x+2y)\,\jhat$ moves a particle along a curve defined by $\rb(t) = (4t+1)\,\ihat + 3t^2\,\jhat$, where $0\le t\le2$ from $(1,0)$ to $(9,12)$. Find the work done if distance is measured in centimeters and force is measured in dynes.

$$ \begin{align*} W = \displaystyle\int_C \rb[F]\cdot d\rb &= \displaystyle\int_C(3x-4y)dx + (4x+2y)dy \\ \\ &= \displaystyle\int_0^2 (3x-4y)x'(t)\,dt + (4x+2y)y'(t)\,dt \\ \\ &= \displaystyle\int_0^2 \left[3(4t+1)-4(3t^2)\right]\,(4)\,dt + \left[4(4t+1)+2(3t^2)\right]\,6t\,dt \\ \\ &= \displaystyle\int_0^2 \left( 3+12t-12t^2\right)4\,dt + \left(4+16t+6t^2\right)6t\,dt \\ \\ &= \displaystyle\int_0^2 \left(12 + 72t + 48t^2 + 36t^3\right)\,dt \\ \\ &= \left[ 12t + 36t^2 + 16t^3 + 9t^4 \right]_0^2 \\ \\ &= 24 + 144 + 128 + 144 = 152 + 288 = 440 \text{ ergs} \end{align*} $$

Your use of this self-initiated mediated course material is subject to our Creative Commons License .

Creative Commons Attribution-NonCommercial-ShareAlike 4.0


Attribution
You must give appropriate credit, provide a link to the license, and indicate if changes were made. You may do so in any reasonable manner, but not in any way that suggests the licensor endorses you or your use.


Noncommercial
You may not use the material for commercial purposes.


Share Alike
You are free to share, copy and redistribute the material in any medium or format. If you adapt, remix, transform, or build upon the material, you must distribute your contributions under the same license as the original.