Math 344: Calculus III

16.6 Parametric Surfaces

---

16.6.1 Parametric Surfaces

A parametric surface is a two-dimensional analogue to a parametric (space) curve. Instead of defining the space curve by a vector function of a single parameter $\mathbf{r}(t)$, we use a vector function of two parameters $\mathbf{r}(u,v)$. This gives us

$$ \def\ihat{\mathbf{\hat{\mmlToken{mi}[mathvariant="bold"]{ı}}}} \def\jhat{\mathbf{\hat{\mmlToken{mi}[mathvariant="bold"]{ȷ}}}} \def\khat{\mathbf{\hat{k}}} \newcommand{\pzi}[2][]{\dfrac{\partial #1}{\partial #2}} \mathbf{r}(u,v) = x(u,v)\,\ihat + y(u,v)\,\jhat + f_z(u,v)\,\khat $$
as the definition of our parametric surface over some two-dimensional region $D$ in the $uv$-plane.

The functions $x$, $y$, and $z$ are all component functions of $\mathbf{r}$ with the set of points given by $(x,y,z)$ defining a surface $\mathbf{S}$ in $\mathbb{R}^3$ with

$$ x = x(u,v)\qquad y = y(u,v) \qquad z = z(u,v) $$
for each $(u,v)\in D$. This $\mathbf{S}$ is the parametric surface and $x$, $y$, and $z$ are the parametric equations of $\mathbf{S}$.

16.6.2 Introductory Examples

Visualizing parametric surfaces can be a little tricky because movement along the surface is controlled by the parameters $u$ and $v$. For a space curve $\mathbf{r}(t)$, things are easier because there is only one parameter so you can think about movement as "forward" for increasing $t$ and "backward" for decreasing $t$. On a parametric surface, you have two dimensions to consider. It is probably easiest to look at both the parameter domain $D$ where $u$ and $v$ are defined alongside the surface to see how they are related.

Let us begin with a simple example to get acquainted with how this works.

Example 1

Plot the parametric surface defined on the region $D = [0, 2\pi]\times [0, 4]$ with the parametrization

$$ \mathbf{r}(u,v) = \cos u\,\ihat + \sin u\,\jhat + v\,\khat. $$

Solution

First, we note that the parameter domain $D$ is a rectangle. Next, we see that $x = \cos u$ and $y = \sin u$, which will be a circle. Lastly, $z = v$ means that movement along the surface in the $y$ direction will occur on vertical lines. Taken all together, this surface is a truncated cylinder with radius 1.

The plots of the parameter domain and the surface in 3D space look like this:

Exercise 1

Identify the surface given by the parametrization

$$ \mathbf{r}(u,v) = \left\langle u\cos v, u\sin v, u^2 \right\rangle $$

Follow Along

This surface is a circular paraboloid in the direction of the $z$-axis. The parameter domain is $\mathbb{R}^2$, since any real input for $u$ and $v$ is valid.

16.6.3 Common Parametric Surfaces

Parametrizations for common surfaces, such as cylinders and spheres are useful to memorize or have a reference for. Here are a few parametric surfaces that show up consistently:

Cylinders

Suppose you have a surface defined by

$$ x^2 + y^2 = r^2\qquad a\leq z \leq b $$
This is a cylinder of radius $r$, and we can use a parametrization inspired by cylindrical coordinates. We want to have two parameters, $\theta$ and $z$ to determine the angular position and height on the cylinder as we do in that system. The radius is fixed, so we do not need a parameter to represent it. It shows up in the parametric equations as a constant.

$$ x = r\cos\theta\qquad y = r\sin\theta\qquad z = z $$
with $\theta\in [0,2\pi]$ and $z\in [a,b]$. This is the general case for Example 1 from above.

Spheres

For a sphere given by

$$ x^2 + y^2 + z^2 = \rho^2 $$
find a parametrization.
We have a sphere of radius $\rho$ centered at the origin. The most straightforward approach is to use spherical coordinates to produce our parametrization. The parameters will be $\varphi$ and $\theta$ representing the same angles that they do in spherical coordinates.

$$ x = \rho\sin\varphi\cos\theta\qquad y = \rho\sin\varphi\sin\theta\qquad z = \rho\cos\varphi $$
with $\varphi\in[0,\pi]$ and $\theta\in[0,2\pi]$ defining the parameter domain. The sphere's radius $\rho$ is a constant, so it will be a positive real number in any particular example.

Planes

Given a position vector $\mathbf{r}_0$ representing the point $P_0$ and nonparallel vectors $\mathbf{a}$ and $\mathbf{b}$, we can parametrize the containing $\mathbf{a}$ and $\mathbf{b}$ that passes through the point $P_0$ by

$$ \mathbf{r}(u,v) = \mathbf{r}_0 + u\mathbf{a} + v\mathbf{b} $$
where $u$ and $v$ can be any real number since the parameter domain is $\mathbb{R}^2$. This gives us a parametrization where any point $P$ may be found on the plane using its position vector $\mathbf{r}(u,v)$.

Surfaces of Revolution

Surfaces of revolution may be easily parametrized. Consider a function $y = f(x)$ with $f(x)\geq 0$ defined on the interval $[a, b]$ and rotate the graph of that function about the $x$-axis to create a surface $S$. This surface has the parametrization

$$ x = x\qquad y = f(x)\cos\theta \qquad z = f(x)\sin\theta $$
where $\theta\in [0,2\pi]$ and $x\in[a,b]$.

16.6.4 Using Technology to Plot Parametric Surfaces

Surfaces with simpler parametrizations like those above have plots that are easier to visualize. More general surfaces may require careful consideration or the use of technology to understand. One very good tool for these visualizations is Geogebra's 3D Calculator (you may need to select 3D Calculator from the drop down list).

There is a very useful feature in this calculator that allows for the plotting of a parametric surface. The function, appropriately enough, is called "surface" and can be used by providing the parameter functions, parameters, and domain for each parameter. Here is an example where a sphere of radius 2 is plotted using this feature:

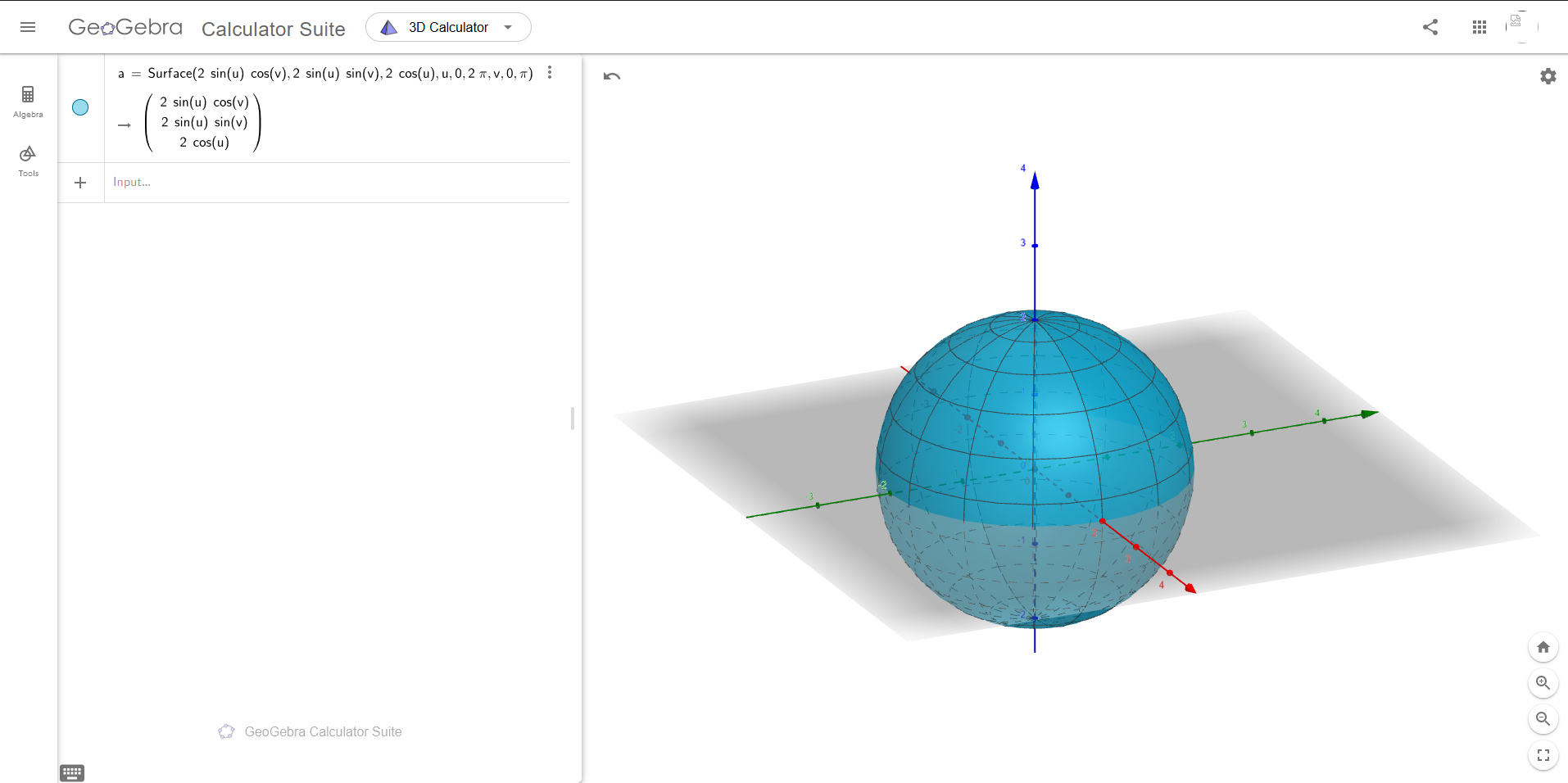
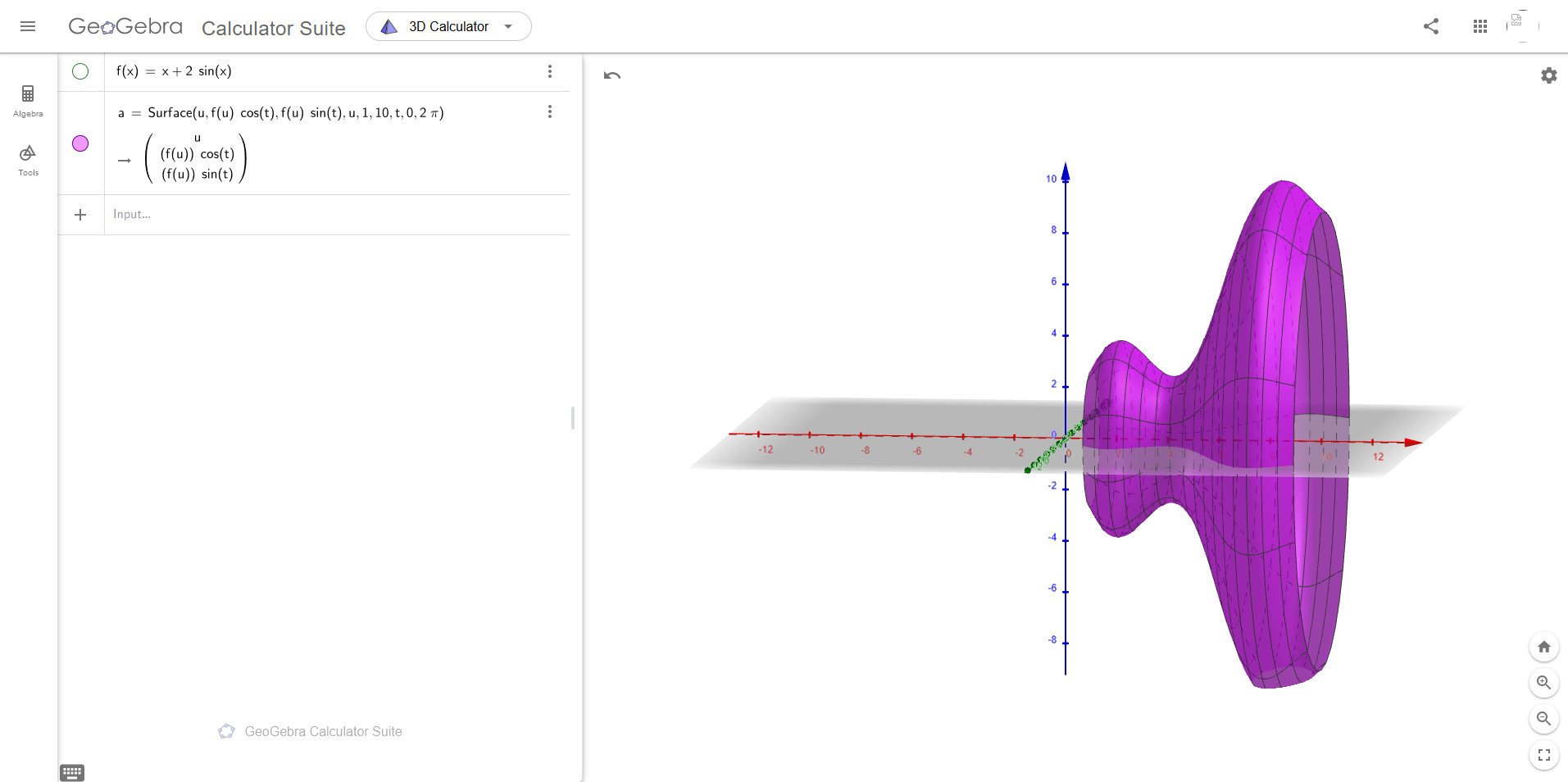
Surfaces of revolution are also easily plotted, as you can define a function $f(x)$ and then use it in the parametrization of the surface. Suppose you have a function $f(x) = x+2\sin (x)$ and you want to plot its surface of revolution for $x\in[1,10]$. You can type $f(x)$'s definition into Geogebra and then use it in the standard parametrization

$$ x = x\qquad y = f(x)\cos\theta \qquad z = f(x)\sin\theta $$

16.6.5 Tangent Planes

The tangent vector to parametric curve came up in many applications, especially the computation of arc length. The plane tangent to a parametric surface is of equal importance. Suppose a surface $S$ is given by the parametrization

$$ \mathbf{r}(u,v) = x(u,v)\,\ihat + y(u,v)\,\jhat + z(u,v)\,\khat $$
where this plane is tangent to $S$ at the point $P_0$ with position vector $\mathbf{r}(u_0,v_0)$.

To find the tangent plane, we use partial derivatives as we did back in Section 14.4 . However, we need to take the partial derivatives of our parameter functions with respect to the parameters. The scheme for this is to hold one of the parameters constant, say $v = v_0$ so that we may differentiate with respect to the other parameter $u$. To differentiate with respect to $v$, we hold $u = u_0$ and take the partials of the parameter functions. We write the following

$$\begin{align*} \mathbf{r}_u &= \pzi[x]{u}(u_0,v_0) +\pzi[y]{u}(u_0,v_0) + \pzi[z]{u}(u_0,v_0) \\ \\ &= x_u(u_0,v_0) + y_u(u_0,v_0) + z_u(u_0,v_0) \\ \\ \mathbf{r}_v &= \pzi[x]{v}(u_0,v_0) + \pzi[y]{v}(u_0,v_0) + \pzi[z]{v}(u_0,v_0) \\ \\ &= x_v(u_0,v_0) + y_v(u_0,v_0) + z_v(u_0,v_0) \end{align*} $$

to represent the plane tangent to $S$ at $P_0$.

The normal vector to this surface is given by $\mathbf{r}_u\times\mathbf{r}_v$, and the surface is considered to be smooth if $\mathbf{r}_u\times\mathbf{r}_v \neq \mathbf{0}$. This cross product being nonzero means that neither $\mathbf{r}_u$ or $\mathbf{r}_v$ are $\mathbf{0}$ and they are not parallel.

Definition

Tangent Plane
The plane tangent to a smooth parametric surface $S$ at a point $P_0$ is the plane containing tangent vectors $\mathbf{r}_u$ and $\mathbf{r}_v$ with normal vector $\mathbf{r}_u\times\mathbf{r}_v$.

Exercise 2

Find an equation for the plane tangent to parametric surface

$$ x = u^2 + 1 \qquad y = v^3 + 1 \qquad z = u + v $$
at the point $(5,2,3)$.

Solution

We begin by writing

$$ \mathbf{r}(u,v) = \left(u^2 + 1\right)\ihat + \left(v^3 + 1\right)\jhat + \left(u+v\right)\khat $$
and note that at the point $(5,2,3)$ our parameters are $u = 2$ and $v = 1$. Next, we compute the tangent vectors

$$ \mathbf{r}_u = 2u\,\ihat + \khat \qquad \qquad \mathbf{r}_v = 3v^2\,\jhat + \khat $$ We recall from Section 12.4 that we may write the equation of a plane using the normal vector, so our next step is compute

$$ \mathbf{r}_u\times\mathbf{r}_v = \begin{vmatrix} \ihat & \jhat & \khat \\ 2u & 0 & 1 \\ 0 & 3v^2 & 1 \end{vmatrix} = \left(-3v^2\right)\ihat - 2u\,\jhat + 6uv^2\,\khat $$
We may now find the tangent vector at $\mathbf{r}(2,1)$, by evaluating the normal vector at $u=2$ and $v=1$:

$$ \mathbf{n} = -3\,\ihat -4\,\jhat + 12\,\khat $$
The scalar equation of the tangent plane is

$$ -3(x-5)-4(y-2)+12(z-3) = 0 \qquad\Rightarrow\qquad 3x + 4y - 12z = -13 $$

16.6.6 Surface Area

With the tangent plane defined, we can begin to investigate the area of a parametric surface. To begin, we choose a parametric surface with a rectangular parameter domain (for simplicity) and divide it into a grid of subrectangles. Labeling these subrectangles $R_{ij}$, we can look at the corresponding "patch" $S_{ij}$ on the surface $S$. Our setup for this involves choosing a point $P_{ij}$ on $S$ given by $\mathbf{r}(u^*_i,v^*_j)$ and looking at the rectangle $R_{ij}$ in our grid given by a small displacement $\Delta u$ and $\Delta v$ from the point $(u^*_i,v^*_i)$ in the parameter domain.

For each patch $S_{ij}$, we take the point $P_{ij}$ to be on a corner. The position vector for $P_{ij}$ is $\mathbf{r}(u^*_i,v^*_j)$, and we approximate this patch with a parallelogram to compute an approximate area. For this parallelogram, we use the partial derivatives of $\mathbf{r}$ and find the tangent vector to the surface at $P_{ij}$, $\left| \mathbf{r}^*_u\times\mathbf{r}^*_v \right| $ with $\mathbf{r}^*_u = \mathbf{r}_u(u^*_i,v^*_j)$ and $\mathbf{r}_v^* = \mathbf{r}_v(u^*_i,v^*_j)$.

The area a parallelogram is given by the magnitude of the tangent vector, so the approximate area for each patch is given by $\left| \mathbf{r}^*_u\times\mathbf{r}^*_v \right| $ and we sum over all choices of these rectangles to determine the integral

$$ \iint_D \left| \mathbf{r}_u\times\mathbf{r}_v \right| dA = \sum_{i=1}^m \sum_{j=1}^n \left| \mathbf{r}^*_u\times\mathbf{r}^*_v \right| \Delta u\Delta v $$
The $\Delta u$ and $\Delta v$ factors are the small corrections for the shape of the surface $S_{ij}$. When we take the limit these corrections become the differentials in the integral notation. Putting this all together:

Definition

Surface Area for a Parametrized Surface
For a smooth parametric surface $S$ given by

$$ \mathbf{r}(u,v) = x(u,v)\,\ihat + y(u,v)\,\jhat + z(u,v)\,\khat \qquad\qquad (u,v)\in D $$
where each point on $S$ has a unique position vector $\mathbf{r}(u,v)$, its surface area is found with the integral

$$ A(S) = \iint_D \left| \mathbf{r}_u\times\mathbf{r}_v \right| dA $$
where the functions

$$ \mathbf{r}_u = \pzi[x]{u}\ihat + \pzi[y]{u}\jhat + \pzi[z]{u}\khat \qquad\qquad \mathbf{r}_v = \pzi[x]{v}\ihat + \pzi[y]{v}\jhat + \pzi[z]{v}\khat $$

Example 2

Suppose you have a sphere of radius 4. Find the area of the spherical cap for the parameter domain

$$ D = \left\{(\varphi,\theta): \left[0,\dfrac{\pi}{4}\right]\times[0,2\pi]\right\} $$

Solution

This surface may be parametrized by

$$ x = 4\sin\varphi\cos\theta\qquad y = 4\sin\varphi\sin\theta\qquad z = 4\cos\varphi $$
where the cross product of the tangent vectors is

$$ \begin{align*} \mathbf{r}_\varphi\times\mathbf{r}_\theta &= \begin{vmatrix} \ihat & \jhat & \khat \\ \pzi[x]{\varphi} & \pzi[y]{\varphi} & \pzi[z]{\varphi} \\ \pzi[x]{\theta} & \pzi[y]{\theta} & \pzi[z]{\theta} \end{vmatrix} \\ \\ &= \begin{vmatrix} \ihat & \jhat & \khat \\ 4\cos\varphi\cos\theta & 4\cos\varphi\sin\theta & -4\sin\varphi \\ -4\sin\varphi\sin\theta & 4\sin\varphi\cos\theta & 0 \end{vmatrix} \\ \\ &= 16\sin^2\!\varphi\cos\theta\,\ihat + 16\sin^2\!\varphi\sin\theta\,\jhat + 16\sin\varphi\cos\varphi\,\khat \end{align*} $$
Now we want to find the magnitude of this vector

$$ \begin{align*} \left|\mathbf{r}_\varphi\times\mathbf{r}_\theta\right| &= \sqrt{64\sin^4\!\varphi\cos^2\!\theta + 64\sin^4\!\varphi\sin^2\!\theta + 64\sin^2\!\varphi\cos^2\!\theta} \\ \\ &= \sqrt{64\sin^4\!\varphi + 64\sin^2\!\varphi\cos^2\!\theta} \\ \\ &= 16\sqrt{\sin^2\!\varphi} = 16\sin\varphi \end{align*} $$
which, unsurprisingly, is very similar to the Jacobian for the transition to spherical coordinates. We can now compute the surface area

$$ \begin{align*} A &= \iint_D \left|\mathbf{r}_\varphi\times\mathbf{r}_\theta\right| dA = \int_0^{2\pi} \int_0^\frac{\pi}{4} 16\sin\varphi\,d\varphi d\theta \\ \\ &= 16\int_0^{2\pi}\! d\theta \int_0^\frac{\pi}{4} \sin\varphi\,d\varphi = 16\left(2\pi\right)\left(\frac{1}{\sqrt{2}}\right) = \dfrac{32\pi}{\sqrt{2}} \end{align*} $$

16.6.7 Surface Area of the Graph of a Function

For the graph of a surface $S$, the parametrization will take the form $z = f(x,y)$ for $(x,y)\in D$ for an $f$ with continuous partial derivatives. We will use the simple choice of $x$ and $y$ for the parameters, so

$$ x = x \qquad y = y \qquad z = f(x,y) $$
and

$$ \mathbf{r}_x = \ihat + \left(\pzi[f]{x}\right)\khat \qquad \qquad \mathbf{r}_y = \jhat + \left(\pzi[f]{y}\right)\khat $$
The tangent vector for the graph of a function is given by

$$ \mathbf{r}_x \times \mathbf{r}_y = \begin{vmatrix} \ihat & \jhat & \khat \\ 1 & 0 & \pzi[f]{x} \\ 0 & 1 & \pzi[f]{y} \end{vmatrix} = -\pzi[f]{x}\ihat - \pzi[f]{y}\jhat + \khat $$
and its magnitude is

$$ \left|\mathbf{r}_x \times \mathbf{r}_y\right| = \sqrt{\left(\pzi[f]{x}\right)^2 + \left(\pzi[f]{y}\right)^2 + 1} $$
In this expression, you can set $z(x,y) = f(x,y)$ if you want to write it that way.

Definition

Surface Area of a Graph of a Function
For a surface $S$ given as the graph of a function $z = f(x,y)$ for $(x,y)\in D$, the surface area is given by

$$ A(S) = \iint_D \sqrt{1 + \left(\pzi[z]{x}\right)^2 + \left(\pzi[z]{y}\right)^2}\, dA $$

Note that this is very similar to the formula for arc length,

$$ L = \int_a^b \sqrt{1 + \left(\dfrac{dy}{dx}\right)^2}\,dx $$

Exercise 3

Find the area of the part of the paraboloid $ z = 4 - x^2 - y^2 $ that lies above the $xy$-plane.

Solution

On the $xy$-plane, $z = 0$ so we have $x^2 + y^2 = 4$ which implies that the maximum radius is 2.

Since we are given this surface in the form of a graph, we have its parametrization for free and may immediately move to computing the surface area.

$$ \begin{align*} A &= \iint_D \sqrt{1 + \left(\pzi[z]{x}\right)^2 + \left(\pzi[z]{y}\right)^2}\, dA \\ \\ &= \iint_D \sqrt{1 + (2x)^2 + (2y)^2}\,dA \\ \\ &= \iint_D \sqrt{1 + 4\left(x^2 + y^2\right)}\,dA \end{align*} $$
The $x^2 + y^2$ term and circular domain makes a switch to polar coordinates natural.

$$ \begin{align*} A &= \int_0^{2\pi} \int_0^2 \sqrt{1 + 4r^2}r\,drd\theta \\ \\ &= \int_0^{2\pi}\! d\theta \int_0^2 r\sqrt{1 + 4r^2}\,dr \\ \\ &= \left.2\pi\left(\frac{1}{8}\right)\frac{2}{3}\left(1 + 4r^2\right)^\frac{3}{2}\right|_{\,0}^{\,2} \\ \\ &= \dfrac{\pi}{6}\left(17\sqrt{17} -1 \right) \end{align*} $$

Your use of this self-initiated mediated course material is subject to our Creative Commons License .

Creative Commons Attribution-NonCommercial-ShareAlike 4.0


Attribution
You must give appropriate credit, provide a link to the license, and indicate if changes were made. You may do so in any reasonable manner, but not in any way that suggests the licensor endorses you or your use.


Noncommercial
You may not use the material for commercial purposes.


Share Alike
You are free to share, copy and redistribute the material in any medium or format. If you adapt, remix, transform, or build upon the material, you must distribute your contributions under the same license as the original.