Math 511: Linear Algebra

Project Exploring Multiplication

---

Table 1

	Test 1	Test 2
Anna	84	96
Bruce	56	72
Chris	78	83
David	82	91

The table shows the first two test scores for Anna, Bruce, Chris, and David. Use the table to create a matrix $M$ to represent the data. Input $M$ into a software program or a graphing utility and use it to answer the questions below.

Using Geogebra one can create a matrix $M$ and plot the scores,

Figure 1

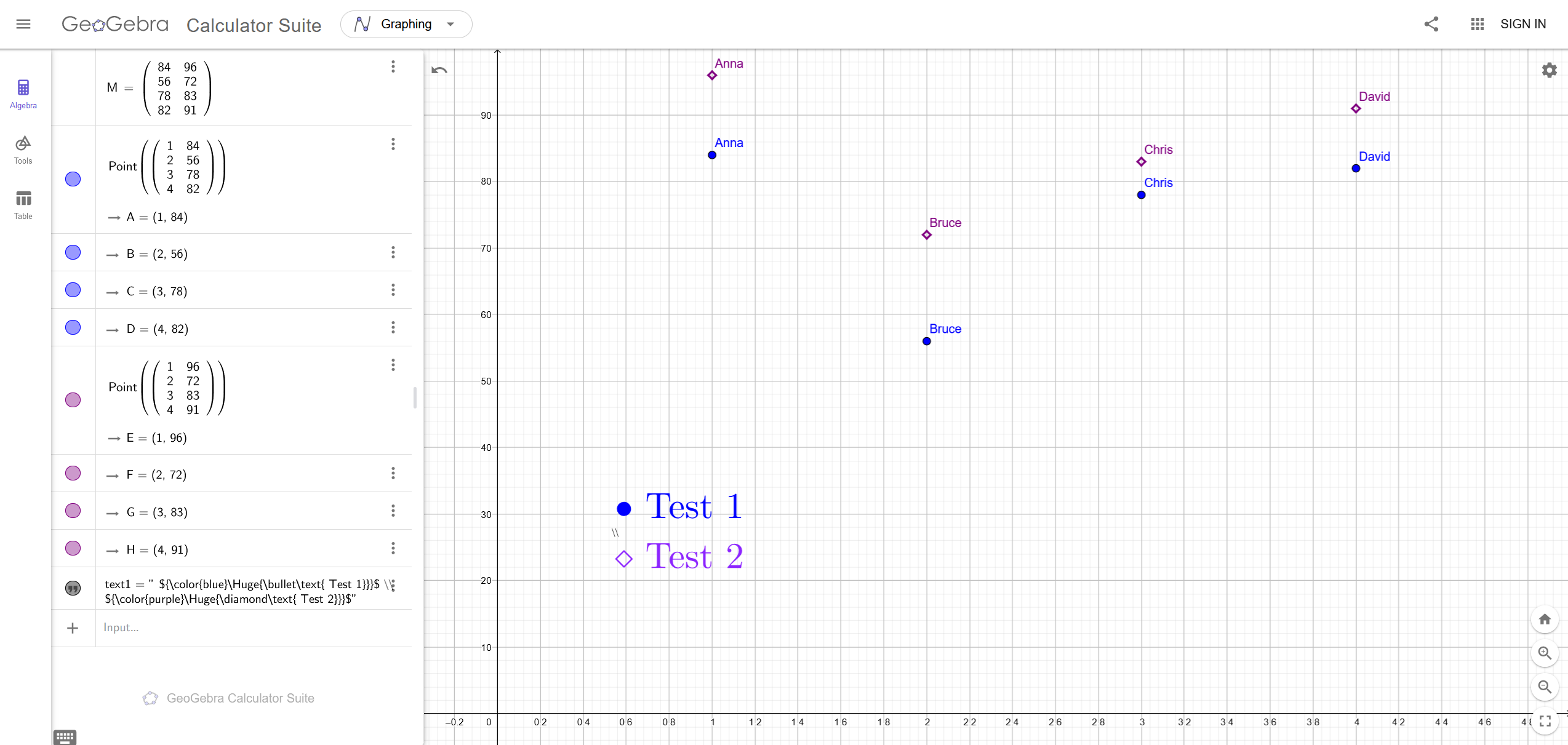
The matrix $M$ has columns ${\color{blue}{\begin{bmatrix} 84\\56\\78\\82 \end{bmatrix}}}$ that represents the ${\color{blue}{\text{Test 1}}}$ scores, and ${\color{purple}{\begin{bmatrix} 96\\72\\83\\91 \end{bmatrix}}}$ that represents the ${\color{purple}{\text{Test 2}}}$ scores.

$$ M = \begin{bmatrix} 84 & 96 \\ 56 & 72 \\ 78 & 83 \\ 82 & 91 \end{bmatrix} $$

1.

Which test was more difficult? Which was easier? Explain.

2.

How would you rank the performances of the four students.

3.

Describe the meanings of the matrix products $M\begin{bmatrix} 1 \\ 0 \end{bmatrix}$ and $M\begin{bmatrix} 0 \\ 1 \end{bmatrix}$. This does not mean describe their algebraic result. Explain what the result represents.

4.

Describe the meanings of the matrix products $\begin{bmatrix} 1 & 0 & 0 & 0 \end{bmatrix}M$ and $\begin{bmatrix} 0 & 0 & 1 & 0 \end{bmatrix}M$

5.

Describe the meaning of the matrix product $M\begin{bmatrix}1\\1\end{bmatrix}$ and $\frac{1}{2}M\begin{bmatrix}1\\1\end{bmatrix}$.

6.

Describe the meanings of the matrix products $\begin{bmatrix} 1&1&1&1 \end{bmatrix}M$ and $\frac{1}{4}\begin{bmatrix} 1&1&1&1 \end{bmatrix}M$

7.

Describe the meaning of the matrix product $\begin{bmatrix} 1 & 1 & 1 & 1 \end{bmatrix}M\begin{bmatrix} 1 \\ 1 \end{bmatrix}$.

8.

Use matrix multiplication to find the combined overall average score on both tests.

9.

How could you use matrix multiplication to scale the scores on test 1 by a factor of 1.1?