Math 511: Linear Algebra
Stochastic Matrices
Stochastic Matrices¶
$$ \require{color} \definecolor{brightblue}{rgb}{.267, .298, .812} \definecolor{darkblue}{rgb}{0.0, 0.0, 1.0} \definecolor{palepink}{rgb}{1, .73, .8} \definecolor{softmagenta}{rgb}{.99,.34,.86} \definecolor{blueviolet}{rgb}{.537,.192,.937} \definecolor{jonquil}{rgb}{.949,.792,.098} \definecolor{shockingpink}{rgb}{1, 0, .741} \definecolor{royalblue}{rgb}{0, .341, .914} \definecolor{alien}{rgb}{.529,.914,.067} \definecolor{crimson}{rgb}{1, .094, .271} \def\ihat{\mathbf{\hat{\unicode{x0131}}}} \def\jhat{\mathbf{\hat{\unicode{x0237}}}} \def\khat{\mathrm{\hat{k}}} \def\tombstone{\unicode{x220E}} \def\contradiction{\unicode{x2A33}} $$
Two companies offer satellite television service to a city. Figure 1 shows the changes in satellite subscriptions each year. The numbers show the portions of the total population of the city.
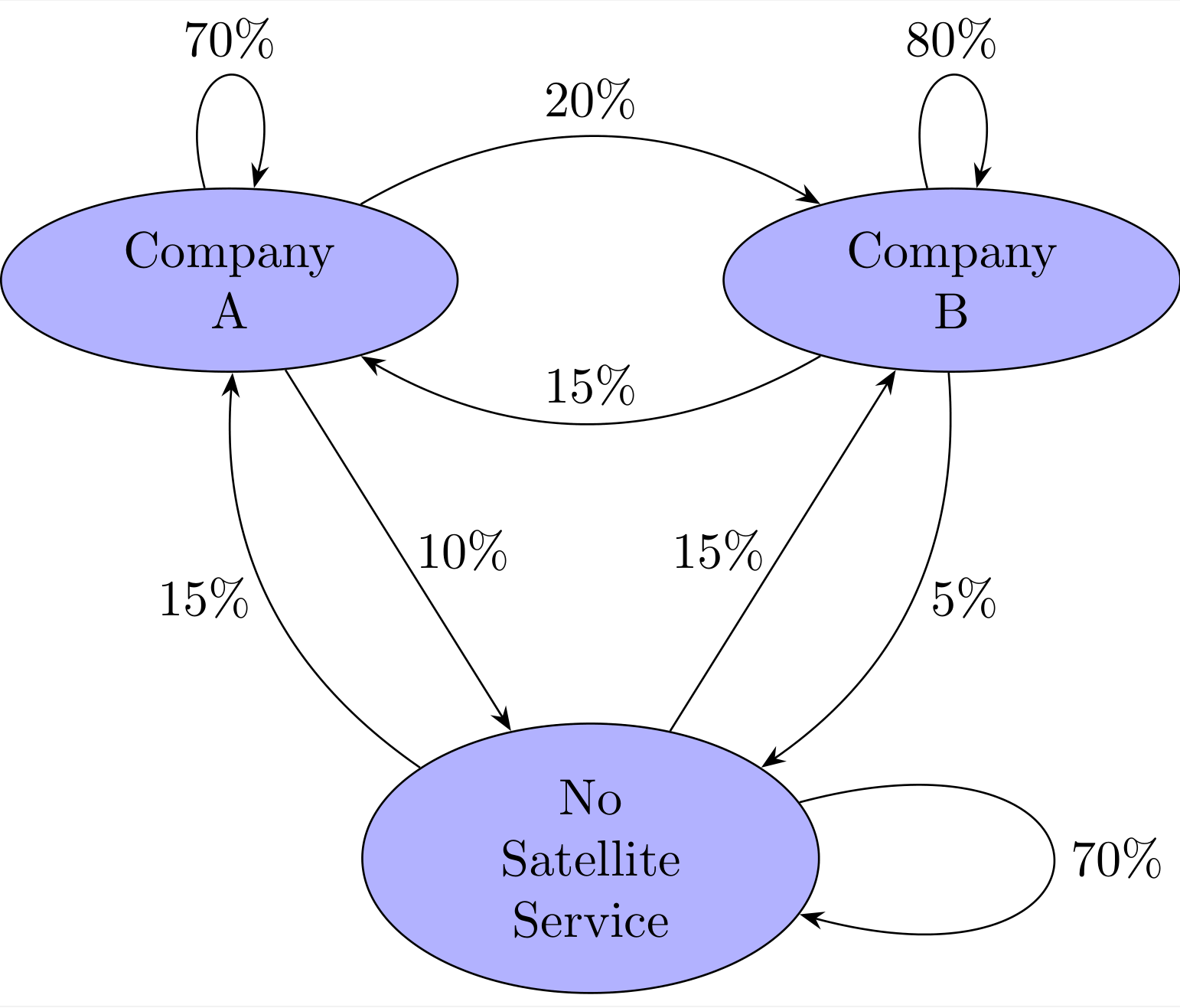
The transition probabilities matrix for the consumer preference model is given by
$$ \begin{align*} &\ \begin{array}{ccc} \quad\ \ \ {\color{red}\text{A}} & \ \ \ \ {\color{red}\text{B}} & \ \ {\color{red}\text{None}} \end{array} \\ P &= \begin{bmatrix} 0.70 & 0.15 & 0.15 \\ 0.20 & 0.80 & 0.15 \\ 0.10 & 0.05 & 0.70 \end{bmatrix} \begin{array}{l} {\color{red} \text{A}} \\ {\color{red} \text{B}} \\ {\color{red} \text{None}} \end{array} \end{align*} $$
The states are
- Subscribing to Company A
- Subscribing to Company B
- No Satellite Television subscription
The initial state vector representing the portions of the total population in each of the three states is
$$ X_0 = \begin{bmatrix} 0.1500 \\ 0.2000 \\ 0.6500 \end{bmatrix} \begin{array}{c} {\color{red} \text{Company A}} \\ {\color{red} \text{Company B}} \\ {\color{red} \text{None}} \end{array} $$
To find the state vector representing the portions of the total population in each state in one year, multiply $P$ by $X_0$ to obtain
$$ X_1 = PX_0 = \begin{bmatrix} 0.70 & 0.15 & 0.15 \\ 0.20 & 0.80 & 0.15 \\ 0.10 & 0.05 & 0.70 \end{bmatrix}\begin{bmatrix} 0.1500 \\ 0.2000 \\ 0.6500 \end{bmatrix} = \begin{bmatrix} 0.2325 \\ 0.2875 \\ 0.4800 \end{bmatrix} $$
After 15 years, the state vector had nearly reached the steady state.
$$ X_{15} = P^{15}X_0 = \begin{bmatrix} 0.3333 \\ 0.4756 \\ 0.1911 \end{bmatrix} $$
For large positive integers $n$, the product $P^nX_0$ reaches a limit $\overline{X}$,
$$ \begin{align*} \overline{X} &= \displaystyle\lim_{n\rightarrow\infty} P^nX_0 \\ P\overline{X} &= \overline{X} = 1\overline{X} \end{align*} $$
For this reason 1 is called an eigenvalue of matrix $P$ with corresponding eigenvector $\overline{X}$.

1.¶
Use a software program like GeoGebra, WolframAlpha, Octave, or MATLAB to compute the eigenvalues and eigenvectors of $P$. We will learn at the end of the course that any nonzero scalar multiple of an eigenvector is also an eigenvector so we have
$$ \begin{array}{lll} {\color{red}\text{Eigenvalue}} & \qquad\qquad{\color{red}\text{Eigenvector}} & \qquad\qquad\qquad\qquad\qquad \end{array} \\ \begin{align*} \lambda_1 &= 1,\qquad \mathbf{x}_1 = \frac{4}{-3.1140e-01}\begin{bmatrix} -5.4495e-01 \\ -7.7850e-01 \\ -3.1140e-01 \end{bmatrix} = \begin{bmatrix} 7 \\ 10 \\ 4 \end{bmatrix} \\ \\ \lambda_2 &= 0.65,\quad \mathbf{x}_2 = \frac{1}{\ \ 7.0771e-01} \begin{bmatrix} 4.9776e-16 \\ -7.0771e-01 \\ 7.0771e-01 \end{bmatrix} = \begin{bmatrix} 0 \\ -1 \\ 1 \end{bmatrix} \\ \\ \lambda_3 &= 0.55,\quad \mathbf{x}_3 = \frac{1}{\ \ 4.0825e-01} \begin{bmatrix} -8.1650e-01 \\ 4.0825e-01 \\ 4.0825e-01 \end{bmatrix} = \begin{bmatrix} -2 \\ 1 \\ 1 \end{bmatrix} \\ \end{align*} $$
Show by computing the products that for $i=1,2,3$, $P\mathbf{x}_i = \lambda_i\mathbf{x}_i$.
2.¶
Let $S$ be the matrix whose columns are the simple eigenvectors of $P$. Show by computing the product that $S^{-1}PS$ is a diagonal matrix $D$. What are the entries along the diagonal of $D$?
3.¶
Show that $P^n = (SDS^{-1})^n = SD^nS^{-1}$. Use this to calculate $X_{15}$ using $D$ and verify the result in the introduction.